а) Выбрать 4 ромашки можно а 3 незабудки - По правилу произведения, составить букет из 7 цветов, в котором 4 ромашки и 3 незабудки можно
ответ
b) Как минимум 4 незабудки это 4 незабудки или 5 незабудки или 6 незабудки или 7 незабудки.. Чувствуется что здесь правило сложения. Четыре незабудки и три ромашки можно Выбрать пять незабудки и две ромашки можно Выбрать шесть цветов незабудки и одна ромашку можно И наконец выбрать семь цветов незабудки можно По правилу сложения, составить букет из 7 цветов, в котором как минимум должны быть 4 незабудки можно 7056 + 3528+672+36=11292
1)√17; возводим в квадрат., получаем 17 Его надо разместить между квадратами целых чисел 1,4,9,16,25,36,49,64,81,100,121 Оно попадает между 16 и 25 16<17<25 √16<√17<√25 4<√17<5 2)√53; то же самое, попадает между 49 и 64 49<53<64 √49<√53<√64 7<√53<64 3)-√3; из особенностей - отрицательный знак. Можно его пока отбросить, и сделат ьвсё как в первых двух примерах 1<3<4 √1<√3<√4 1<√3<2 и теперь меняем знаки -2<-√3<-1 4)√323; Какие большие числа... считаем корень из 323 на калькуляторе, получаем 17,97 Значит 17<√323<18 Но можно и дальше продлить таблицу квадратов, как в первом примере 5)-√212; корень из 212 = 14,56 -15<-√212<14 6)√170; 169<170<196 13<√170<14 8)-√200. 196<200<225 14<√200<15 -15<-√200<-14
а) Выбрать 4 ромашки можно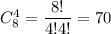 а 3 незабудки -
а 3 незабудки - 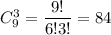 По правилу произведения, составить букет из 7 цветов, в котором 4 ромашки и 3 незабудки можно
По правилу произведения, составить букет из 7 цветов, в котором 4 ромашки и 3 незабудки можно 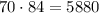
ответ
b) Как минимум 4 незабудки это 4 незабудки или 5 незабудки или 6 незабудки или 7 незабудки.. Чувствуется что здесь правило сложения. Четыре незабудки и три ромашки можно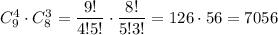 Выбрать пять незабудки и две ромашки можно
Выбрать пять незабудки и две ромашки можно 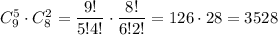 Выбрать шесть цветов незабудки и одна ромашку можно
Выбрать шесть цветов незабудки и одна ромашку можно 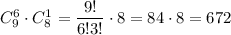 И наконец выбрать семь цветов незабудки можно
И наконец выбрать семь цветов незабудки можно 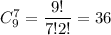 По правилу сложения, составить букет из 7 цветов, в котором как минимум должны быть 4 незабудки можно 7056 + 3528+672+36=11292
По правилу сложения, составить букет из 7 цветов, в котором как минимум должны быть 4 незабудки можно 7056 + 3528+672+36=11292
ответ: 11292.
возводим в квадрат., получаем 17
Его надо разместить между квадратами целых чисел
1,4,9,16,25,36,49,64,81,100,121
Оно попадает между 16 и 25
16<17<25
√16<√17<√25
4<√17<5
2)√53;
то же самое, попадает между 49 и 64
49<53<64
√49<√53<√64
7<√53<64
3)-√3;
из особенностей - отрицательный знак. Можно его пока отбросить, и сделат ьвсё как в первых двух примерах
1<3<4
√1<√3<√4
1<√3<2
и теперь меняем знаки
-2<-√3<-1
4)√323;
Какие большие числа...
считаем корень из 323 на калькуляторе, получаем 17,97
Значит
17<√323<18
Но можно и дальше продлить таблицу квадратов, как в первом примере
5)-√212;
корень из 212 = 14,56
-15<-√212<14
6)√170;
169<170<196
13<√170<14
8)-√200.
196<200<225
14<√200<15
-15<-√200<-14