из а в в од­но­вре­мен­но вы­еха­ли два ав­то­мо­би­ли­ста. пер­вый про­ехал с по­сто­ян­ной ско­ро­стью весь путь. вто­рой про­ехал первую по­ло­ви­ну пути со ско­ро­стью, мень­шей ско­ро­сти пер­во­го ав­то­мо­би­ли­ста на 20 км/ч, а вто­рую по­ло­ви­ну пути про­ехал со ско­ро­стью 117 км/ч, в ре­зуль­та­те чего при­был в в од­но­вре­мен­но с пер­вым ав­то­мо­би­ли­стом. най­ди­те ско­рость пер­во­го ав­то­мо­би­ли­ста, если из­вест­но, что она боль­ше 70 км/ч.

23.17
p(x)=(2х+1)(4х^2-2х+1)-8х^3=(8х^3-4x^2+2x+4x^2-2x+1)-8x^3=1
То есть при любых значениях х ответ будет всегда 1.

23.18р(х;у)=(ху+3)(2ху-4)-2(ху-7)=2*x^2*y^2-4xy+6xy-12-2xy+14=2*x^2*y^2+2
Разберем по частям 2*x^2*y^2+2
1)
2*x^2*y^2 всегда положителен, так как квадрат числа не может быть отрицательным, положительное число{2}умножаем{x^2}и умножаем на {y^2} = положительное число, всегда положителен
2)
число 2>0, положительное число 
3) сумма двух положительных чисел {2*x^2*y^2 и 2} всегда дает нам положительное число

Объяснение:

Уравнение вида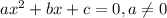    называется квадратным уравнением.

а) Если один из коэффициентов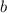 или с  равен нулю, то уравнение называется неполным . Данное уравнение неполное квадратное уравнение.

б) старший коэффициент а= 4;

второй коэффициент b= 16;

свободный член с= 0

в) решим данное уравнение. Для этого вынесем 4х ха скобки и разложим  левую часть уравнения на множители.

Произведение равно нулю, если хотя бы один из множителей равен нулю, а другой при этом определен

х=0    или      х+4=0

                      х= - 4

Данное уравнение имеет два корня - 4 и 0 .