Из цифр 1 2 5 7 8 9 составлены всевозможные пятизначные числа без повторения цифр. Сколько среди этих чисел таких, которые кратны И ОТМЕЧУ КАК ЛУЧШИЙ)
1.)Предприятие изготовило за квартал 500 насосов, из которых 60% имели высшую категорию качества. Сколько насосов высшей категории качества изготовило предприятие?
Решение:
Найдем 60% от 500 (общее количество насосов).
60 % = 0,6
500 · 0,6 = 300 насосов высшей категории качества.
ответ: 300 насосов высшей категории качества.
2.). За месяц на предприятии изготовили 500 приборов. 20% изготовленных приборов не смогли пройти контроль качества. Сколько приборов не контроль качества? Решение. Нужно найти 20% от общего количества изготовленных приборов 20% = 0,2. 500 * 0,2 = 100. 100 из общего количества изготовленных приборов контроль не Готовясь к экзамену, школьник решил 38 задач из пособия для самоподготовки. Что составляет 23% числа всех задач в пособии. Сколько всего задач собрано в этом пособии для самоподготовки? Решение. Мы не знаем, сколько всего задача в пособии. Но зато нам известно, что 38 задач составляют 25% от общего их количества. Запишем 23% в виде дроби: 0,23. Далее нам следует известную нам часть целого разделить на ту долю, которую она составляет от всего целого: 38/0,25 = 38 * 100/25 = 152. Именно 152 задачи включили в этот сборник. 4.) В классе 30 учеников. 14 из них – девочки. Сколько процентов девочек в классе? Решение. Чтобы узнать, какой процент составляет одно число от другого, нужно то число, которое требуется найти, разделить на общее количество и умножить на 100%. Значит, 14/30*100% = 7/15*100% = 7*100%/15 = 47%.
Подходят интервалы, где стоит минус. Знак неравенства строгий - значит сами точки не берем. + добавляем ОДЗ. Получаем
x∈( -∞;-4.5)∪(-2;0)∪(0;2) - нужно целое неотрицательное значение x=1
5) x³-8x√x+18>0
(x√x)²-2*4*x√x+4²+2>0
(x√x-4)²+2>0
Квадрат (x√x-4)² - при любых неотрицательных x является неотрицательным числом - в нему добавляют 2 - значит получают строго положительное число . Доказали :)
Решение:
Найдем 60% от 500 (общее количество насосов).
60 % = 0,6
500 · 0,6 = 300 насосов высшей категории качества.
ответ: 300 насосов высшей категории качества.
2.). За месяц на предприятии изготовили 500 приборов. 20% изготовленных приборов не смогли пройти контроль качества. Сколько приборов не контроль качества?
Решение. Нужно найти 20% от общего количества изготовленных приборов 20% = 0,2. 500 * 0,2 = 100. 100 из общего количества изготовленных приборов контроль не Готовясь к экзамену, школьник решил 38 задач из пособия для самоподготовки. Что составляет 23% числа всех задач в пособии. Сколько всего задач собрано в этом пособии для самоподготовки?
Решение. Мы не знаем, сколько всего задача в пособии. Но зато нам известно, что 38 задач составляют 25% от общего их количества. Запишем 23% в виде дроби: 0,23. Далее нам следует известную нам часть целого разделить на ту долю, которую она составляет от всего целого: 38/0,25 = 38 * 100/25 = 152. Именно 152 задачи включили в этот сборник.
4.) В классе 30 учеников. 14 из них – девочки. Сколько процентов девочек в классе?
Решение. Чтобы узнать, какой процент составляет одно число от другого, нужно то число, которое требуется найти, разделить на общее количество и умножить на 100%. Значит, 14/30*100% = 7/15*100% = 7*100%/15 = 47%.
3) x=1
Объяснение:
3)
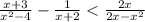ОЗД: x≠0, x≠2, x≠-2
Методом интервалов находим знаки выражения:
- + - +
-----------------°-------------°----------°---------------------->
-∞ -4.5 -2 2 +∞
Подходят интервалы, где стоит минус. Знак неравенства строгий - значит сами точки не берем. + добавляем ОДЗ. Получаем
x∈( -∞;-4.5)∪(-2;0)∪(0;2) - нужно целое неотрицательное значение x=1
5) x³-8x√x+18>0
(x√x)²-2*4*x√x+4²+2>0
(x√x-4)²+2>0
Квадрат (x√x-4)² - при любых неотрицательных x является неотрицательным числом - в нему добавляют 2 - значит получают строго положительное число . Доказали :)