Из кассы выдано 3/11 всех имеющихся денег, потом 1/4 остатка, далее 2/7 нового остатка и, наконец, 7/9 третьего остатка, после этого в кассе осталось 660000 рублей. Сколько денег было в кассе первоначально?
Обратная матрица отыскивается так: к начальной матрице приписывается справа единичная, получаем матрицу 3х6. Затем линейными преобразованиями строк добиваемся единичной матрицы слева. Тогда справа будет обратная матрица: Первый переход: вычитаем упятерённую первую строку из второй и учетверённую первую из третьей Второй переход: вычитаем вторую строку из первой, делим вторую строку пополам, вычитаем вторую строку из третьей Третий переход: вычитаем утроенную третью строку из первой, увеличиваем третью строку в 2 раза, прибавляем учетверённую третью строку к первой. Получаем:
где |A| - определитель матрицы, а - транспонированная матрица алгебраических дополнений
Т.к. определитель матрицы не равен 0, то обратная матрица существует.
Находим матрицу миноров. Для каждого элемента матрицы соответствующий ему минор вычисляется по определителю матрицы 2х2, которая получается вычеркиванием соответствующей строки и столбца для этого элемента:
Получили следующую матрицу миноров:
Из матрицы миноров получим матрицу алгебраических дополнений заменой знака на противоположный у элементов матрицы миноров, у которых сумма номеров строк и столбца нечетна:
Следующим шагом получаем транспонированную матрицу алгебраических дополнений:
Обратная матрица:
Проверим, что произведение исходной и обратной матрицы равно единичной:
Первый переход: вычитаем упятерённую первую строку из второй и учетверённую первую из третьей
Второй переход: вычитаем вторую строку из первой, делим вторую строку пополам, вычитаем вторую строку из третьей
Третий переход: вычитаем утроенную третью строку из первой, увеличиваем третью строку в 2 раза, прибавляем учетверённую третью строку к первой. Получаем:
Обратную матрицу найдем по формуле:
где |A| - определитель матрицы, а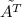 - транспонированная матрица алгебраических дополнений
- транспонированная матрица алгебраических дополнений
Т.к. определитель матрицы не равен 0, то обратная матрица существует.
Находим матрицу миноров. Для каждого элемента матрицы соответствующий ему минор вычисляется по определителю матрицы 2х2, которая получается вычеркиванием соответствующей строки и столбца для этого элемента:
Получили следующую матрицу миноров:
Из матрицы миноров получим матрицу алгебраических дополнений заменой знака на противоположный у элементов матрицы миноров, у которых сумма номеров строк и столбца нечетна:
Следующим шагом получаем транспонированную матрицу алгебраических дополнений:
Обратная матрица:
Проверим, что произведение исходной и обратной матрицы равно единичной: