из натуральных чисел от 1 до 45 ученик назвал одно число Какова вероятность того что это число будет делителем 30? с решением

Показать ответ

Ответ:

zulyarakhimovaa

18.06.2022 19:56

$1)\ \ y=\left\{\begin{array}{ll}2x-6\ ,\ \ esli\ x\geq 3\ ,\\6-2x\ ,\ \ esli\ x$

График кусочно-линейной функции состоит из нескольких частей (кусочков). Функция задаётся разными аналитическими выражениями на различных промежутках. Вне указанных промежутков линии либо стираются, либо рисуются штриховыми линиями .

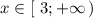На промежутке $x\in [\ 3;+\infty \, )$ рисуем прямую у=2х-6. Она проходит через точки (3;0) и (6;6) . Вне этого промежутка линия нарисована штрихом, но её можно и стереть. Точка (3;0) принадлежит этой прямой, так как х=3 входит в указанный промежуток.

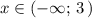На интервале $x\in (-\infty ;\, 3\, )$ рисуем прямую у=6-2х . Она проходит через точки (3;0) и (0;6) . Вне этого промежутка линия нарисована штрихом, но её можно и стереть. Точка (3:0) не принадлежит этой прямой.

График нарисован сплошными линиями .

$2)\ \ y=\left\{\begin{array}{ll}3-2x\ ,\ esli\ \ x\geq -1\ ,\\5\ \ ,\ \ esli\ \ x$

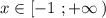Строим прямую у=3-2х , проходящую через точки (-1;5) и (1;1) , на промежутке $x\in [-1\ ;+\infty \, )$ . Точка (-1;6) принадлежит графику .

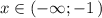Прямая у=5 - это прямая, параллельная оси ОХ, проходящая через точку (0;5) . Строим её на интервале $x\in (-\infty ;-1\, )$ . Точка (-1;5) не принадлежит графику .

График нарисован сплошными линиями .

$3)\ \ y=\left\{\begin{array}{lll}2x+1\ ,\ esli\ ,\ x\geq 3\ ,\\7\ ,\ esli\ ,\ -4\leq x$

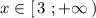Строим прямую у=2х+1 , проходящую через точки (3;7) и (5;11) , на промежутке $x\in [\, 3\ ;+\infty \, )$ . Точка (3;7) принадлежит графику .

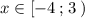Прямая у=7 - это прямая, параллельная оси ОХ, проходящая через точку (0;7) . Строим её на промежутке $x\in [-4\, ;\, 3\, )$ . Точка (-4;7) принадлежит графику , а точка (3;7) не принадлежит графику .

Прямую у=-2х-1 , проходящую через точки (-4;7) и (-7;13) , строим на промежутке $x\in (-\infty ;\, -4\ ]$ . Точка (-4;7) не принадлежит графику .

График нарисован сплошными линиями .

$4)\ \ y=\left\{\begin{array}{lll}2-x\ ,\ esli\ ,\ x\geq -1,5\ ,\\3x+8\ ,\ esli\ ,\ -5\leq x$

Прямую у=2-х , проходящую через точки (-1,5; 3,5) и (2;0) , строим на промежутке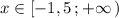 $x\in [-1,5\, ;+\infty \, )$ . Точка (-1,5; 3,5) принадлежит графику .

Прямую у=3х+8 , проходящую через точки (-1,5; 3,5) и (-5;-7) , строим на промежутке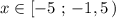 $x\in [-5\ ;\, -1,5\, )$ . Точка (-1,5; 3,5) не принадлежит графику .

Прямую у=х-2 , проходящую через точки (-5; -7) и (-10;-12) , строим на промежутке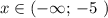 $x\in (-\infty ;\, -5\ )$ . Точка (-5; -7) не принадлежит графику .

График нарисован сплошными линиями . На последнем рисунке нарисован заданный график без штриховых линий.

,под всеми буквами. С подробным объяснением !

0,0(0 оценок)

Ответ:

vvvtalik3

01.05.2022 05:28

Объяснение:

Имеем функцию:

y = 5 - 2 * sin^2 (2x).

Для нахождения наименьшего и наибольшего значений функции стоит отметить, что тригонометрическая функция синуса аргумента независимо от значения своего аргумента принимает значения, находящиеся в промежутке [-1; 1]. Запишем область значений в виде двойного неравенства:

-1 <= sin 2x <= 1;

Возводим в квадрат части неравенства:

0 <= sin^2 2x <= 1;

Умножим все части на минус два:

-2 <= -2 * sin^2 2x <= 0;

Прибавим ко всем частям неравенства пять:

3 <= 5 - 2 * sin^2 2x <= 5.

3 и 5 - наименьшее и наибольшее значения функции.

0,0(0 оценок)

Популярные вопросы: Алгебра