Из пункта А в пункт В расстояние между которыми 210 км вышел катер. дойдя до пункта В,он вернулся в пункт отправления, затратив на обратный путь на 4 часа меньше. Найдите собственную скорость катера, если скорость течения реки равна 3 км/ч. ответ дайте в км/ч.
1. нет; 2. 1) общего вида 2) общего вида 3) общего вида 3. 1) -1; 3 2) 1; -3 4) -1
Объяснение:
1. Если функция нечетная то произведение f(3)f(-3) не будет положительным.
2.
1)
Это функция общего вида
2)
Это функция общего вида
3)
Это функция общего вида
3.
1)
Значит
2)
Значит
4.
Это биквадратное уравнение. Делаем подстановку
Уравнение будет иметь один корень, когда дискриминант равен 0
Но, поскольку х=±√у, то при любом положительном у мы получим два различных значения х. Одно значение х мы получим лишь в случае у=0. Тогда х=√0=0. Следовательно
Делаем проверку:
1) а=-1
Имеется одно решение (т.к выражение в скобках никогда не будет равно 0)
2) а=3
Здесь появляется второй корень. Значит, это значение не подходит.
Окончательно получаем решение: а=-1
Раскладываем вторую скобку по формуле разности кубов
Заметим, что неполный квадрат в третьей скобке всегда положителен
Докажем это
Так как квадраты не могут быть отрицательными.
Значит можно рассмотреть неравенство методом интервалов.
1) При х<0 первый множитель будет меньше нуля, второй тоже меньше нуля. Два множителя меньше нуля дадут положительное число. А третий будет положительным. Значит все выражение в левой части будет положительным.
2) При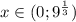 Первый множитель будет больше нуля, второй меньше нуля, а третий как всегда положителен. Отрицательный множитель помноженный на положительные множители даст в итоге отрицательное число.
Первый множитель будет больше нуля, второй меньше нуля, а третий как всегда положителен. Отрицательный множитель помноженный на положительные множители даст в итоге отрицательное число.
3)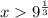
Первый множитель будет положителен, второй тоже положителен. А третий как всегда положителен. Значит в итоге, перемножив три положительных числа, получим положительное число.
В ответе получим два промежутка из первого и третьего случаев.
Заметно, что целочисленных решений будет бесконечно много. Это и все отрицательные целые числа и целые числа большие 2. Так как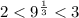
Решений, так сказать, счетное множество.
Ну, а если бы был бы в неравенстве противоположный знак, то было бы всего два решения из второго случая. Это числа 1 и 2.