Когда мы видим уравнения с x и y в квадрате и с одинаковыми коэффициентами перед ними, это наводит на мысль, что перед нами уравнение окружности. Оно имеет вид . Попробуем преобразовать его к данному виду. Для этого нужно поделить обе части на 2, чтобы коэффициент при старших членах был 1, и выделить полные квадраты:
Это окружность с радиусом . Если радиус равен нулю, то окружность превращается в точку. Значит, окружности не существует, если не выполняется ОДЗ корня: .
Можно было рассуждать немного иначе: провести те же самые преобразования, но рассуждать не в терминах окружности, а в терминах суммы. В левой части сумма двух квадратов, каждый из них не меньше нуля. Значит, вся левая часть не меньше нуля, причём слагаемые друг от друга не зависят, поэтому в левой части можно представить любое неотрицательное число. Но тогда и правая часть не меньше нуля. Если же правая часть меньше нуля, то пара (x; y) не найдётся.
a < 0
Объяснение:
Когда мы видим уравнения с x и y в квадрате и с одинаковыми коэффициентами перед ними, это наводит на мысль, что перед нами уравнение окружности. Оно имеет вид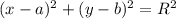
. Попробуем преобразовать его к данному виду. Для этого нужно поделить обе части на 2, чтобы коэффициент при старших членах был 1, и выделить полные квадраты:
Это окружность с радиусом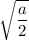
. Если радиус равен нулю, то окружность превращается в точку. Значит, окружности не существует, если не выполняется ОДЗ корня: 
.
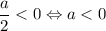Можно было рассуждать немного иначе: провести те же самые преобразования, но рассуждать не в терминах окружности, а в терминах суммы. В левой части сумма двух квадратов, каждый из них не меньше нуля. Значит, вся левая часть не меньше нуля, причём слагаемые друг от друга не зависят, поэтому в левой части можно представить любое неотрицательное число. Но тогда и правая часть не меньше нуля. Если же правая часть меньше нуля, то пара (x; y) не найдётся.
тебе надо график,или упростить?
выбери сам:
Найдем точки минимума и максимума
y' = 3x^2 - 12 = 3(x^2 - 4) = 3(x + 2)(x - 2) = 0
y(-2) = -8 + 24 - 4 = 12 - максимум
y(2) = 8 - 24 - 2 = -18 - минимум.
Значит, один корень x1 лежит на промежутке (-2, 2)
Найдем значения еще в нескольких точках
y(0) = -4
y(-1) = -1 + 12 - 4 = 7
-1 < x1 < 0
y(-3) = -27 + 36 - 4 = 5
y(-4) = -64 + 48 - 4 = -20
-4 < x2 < -3
y(3) = 27 - 36 - 4 = -13
y(4) = 64 - 48 - 4 = 12
3 < x3 < 4
Дальше подставляешь промежуточные значения и уточняешь результат.
x1 ~ -0,3; y(-0,3) ~ -0,4
x2 ~ -3,3; y(-3,3) ~ -0,3
x3 ~ 3,6; y(3,6) ~ -0,5
При желании можно уточнить до сотых долей.