Еслть формула для площади параллелограмма
У прямоугольника диагонали равны, так что прямоугольник с наибольшей площадью тот, у кого угол между диагоналями прямой (т.е. этот прямоугольник - квадрат).
со всех читырёхугольников самую большую площу имеет квадрат (прямоугольник с равными сторонами)
площу можна найти по формуле
S=a*a
S=d*d\2
d=18 - диагональ
18*18\2=162
S=162
a - сторона
а=162 под корень
а=12,7
Еслть формула для площади параллелограмма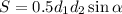
У прямоугольника диагонали равны, так что прямоугольник с наибольшей площадью тот, у кого угол между диагоналями прямой (т.е. этот прямоугольник - квадрат).
со всех читырёхугольников самую большую площу имеет квадрат (прямоугольник с равными сторонами)
площу можна найти по формуле
S=a*a
S=d*d\2
d=18 - диагональ
18*18\2=162
S=162
a - сторона
а=162 под корень
а=12,7