Решаем второе уравнение: x1 = 1; x2 = -2. Подставляем в первое: 1)3-2+с = 0; с = - 1; 2)12 +4 +с = 0; с = 16; Положения относительно оси Х уравнения имеют разные, а параметр с влияет только на положение по оси Y. Изменяя с, мы приближаем или отдаляем корни от координаты X вершины, но переместить через эту координату - не можем. Значит, если с одной стороны от x координаты точки максимума 2 корня, то с другой их нет, если один, то второй при условии его сеществования, будет с другой стороны от координаты. Поэтому может быть только ситуация с одним общим корннем за раз, значит максимальное кол-во значеений с параметра - 2.
Объяснение:
1) (x-6)*(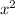 +6x+36)=
+6x+36)=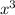 -
-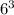 =
=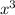 -216 в)
-216 в)
2) это я не совсем понимаю
3) (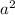 +2
+2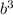 )*(
)*(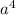 -2
-2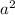
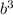 +4
+4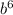 )=(
)=(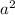 )в кубе+(2
)в кубе+(2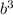 )в кубе=
)в кубе=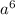 +8
+8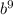 г)
г)
4) 3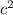 -48=3(
-48=3(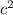 -16)=3(c-4)(c+4) б)
-16)=3(c-4)(c+4) б)
5) 7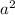 -42a+63=7(
-42a+63=7(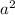 -6a+9)=7(a-3)в квадрате б)
-6a+9)=7(a-3)в квадрате б)
6)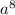 -
-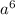 =
=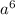 (
(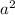 -1)=
-1)=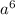 (a-1)(a+1) б)
(a-1)(a+1) б)
7)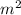 -
-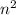 +m+n=(m-n)(m+n)+m+n=(m+n)(m-n+1) а)
+m+n=(m-n)(m+n)+m+n=(m+n)(m-n+1) а)
8)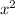 -
-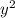 +14y-49=
+14y-49=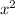 -(
-(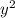 -14y+49)=
-14y+49)=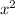 -(y-7)в квадрате=(x-(y-7))(x+(y-7))=(x-y+7)(x+y-7) в)
-(y-7)в квадрате=(x-(y-7))(x+(y-7))=(x-y+7)(x+y-7) в)
9) 81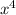 -1=(9
-1=(9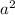 -1)(9
-1)(9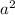 +1)=(3a-1)(3a+1)(9
+1)=(3a-1)(3a+1)(9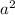 +1) а)
+1) а)
10) 49x-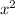 =0
=0
x(49-x)=0
x=0 49-x=0
x=49
в)
11)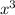 +3
+3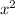 -x-3=0
-x-3=0
(x+3)(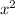 -1)=0
-1)=0
x+3=0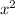 -1=0
-1=0
x=-3 x=-1 або x=1
г)
12) насчёт этого не уверена
(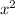 -2)в квадрате-4(
-2)в квадрате-4(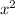 -2)+4=(
-2)+4=(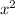 -2-2)в квадрате=(
-2-2)в квадрате=(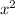 -4)в квадрате=((x-2)*(x+2))в квадрате
-4)в квадрате=((x-2)*(x+2))в квадрате