Известно, что график функции проходит через точку (k;6). Дана функция: f(x)=-х2- х+12; а) Найдите значения функции f(3), f(-5) b) Найдите значение k. с) Постройте график.
Чтобы изобразить график линейной функции вида где и — коэффициенты, достаточно на координатной плоскости отметить две точки и провести через них прямую.
Для этого строят таблицу для двух точек: первая строка — абсцисса (иксы), вторая строка — ордината (игреки). Вы — хозяин своей таблицы. Подбирайте любое значение подставляйте его в функцию и находите (Подбирайте числа в пределах разумного.)
Пример. Изобразить график линейной функции
Строим таблицу для двух точек:
Пусть
Тогда
Пусть
Тогда
Имеем заполненную таблицу для двух точек. Изобразим координатную плоскость, отметим две точки: и — и проведем через них прямую (см. вложение). График линейной функции построен.
1)3%(x-2)<3³ x-2<3 x<5 x∈(-∞;5) 2)ОДЗ 3x-7>0⇒3x>7⇒x>7/3 3x-7<2 3x<9 x<3 x∈(7/3;3) 3)4^(x²)<4² x²<2 (x-√2)(x+√2)<0 x=√2 x=-√2 x∈(-√2;√2) 4)ОДЗ x²-5x-6>0 x1+x2=5 U x1*x2=-6⇒x1=-1 U x2=6 x<-1 U x>6 x²-5x-6≤8 x²-5x-14≤0 x1+x2=5 U x1*x2=-14⇒x1=-2 U x2=7 -2≤x≤7 x∈[-2;-1) U (6;7] 5)ОДЗ (3x-2)/(2x²+1)>0 2x²+1>0 при любом х⇒3x-2>0⇒3x>2⇒x>2/3 (3x-2)/(2x²+1)>1 (3x-2)/(2x²+1)-1>0 (3x-2-2x²-1)/(2x²+1)>0 (2x²-3x+3)/(2x²+1)<0 2x²+1>0 при любом х⇒2x²-3x+3<0 D=9-24=-15<0 решения нет
Чтобы изобразить график линейной функции вида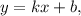 где
где 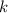 и
и 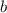 — коэффициенты, достаточно на координатной плоскости отметить две точки и провести через них прямую.
— коэффициенты, достаточно на координатной плоскости отметить две точки и провести через них прямую.
Для этого строят таблицу для двух точек: первая строка — абсцисса (иксы), вторая строка — ордината (игреки). Вы — хозяин своей таблицы. Подбирайте любое значение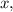 подставляйте его в функцию и находите
подставляйте его в функцию и находите 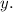 (Подбирайте числа в пределах разумного.)
(Подбирайте числа в пределах разумного.)
Пример. Изобразить график линейной функции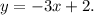
Строим таблицу для двух точек:
Пусть
Тогда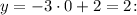
Пусть
Тогда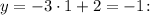
Имеем заполненную таблицу для двух точек. Изобразим координатную плоскость, отметим две точки: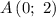 и
и 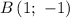 — и проведем через них прямую (см. вложение). График линейной функции
— и проведем через них прямую (см. вложение). График линейной функции 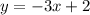 построен.
построен.
x-2<3
x<5
x∈(-∞;5)
2)ОДЗ 3x-7>0⇒3x>7⇒x>7/3
3x-7<2
3x<9
x<3
x∈(7/3;3)
3)4^(x²)<4²
x²<2
(x-√2)(x+√2)<0
x=√2 x=-√2
x∈(-√2;√2)
4)ОДЗ x²-5x-6>0
x1+x2=5 U x1*x2=-6⇒x1=-1 U x2=6
x<-1 U x>6
x²-5x-6≤8
x²-5x-14≤0
x1+x2=5 U x1*x2=-14⇒x1=-2 U x2=7
-2≤x≤7
x∈[-2;-1) U (6;7]
5)ОДЗ (3x-2)/(2x²+1)>0
2x²+1>0 при любом х⇒3x-2>0⇒3x>2⇒x>2/3
(3x-2)/(2x²+1)>1
(3x-2)/(2x²+1)-1>0
(3x-2-2x²-1)/(2x²+1)>0
(2x²-3x+3)/(2x²+1)<0
2x²+1>0 при любом х⇒2x²-3x+3<0
D=9-24=-15<0
решения нет