Число р при делении на 3 может давать остатки 0,1 или 2.
Если число р при делении на 3 дает остаток 1, то оно имеет вид
p=3k+1, где k - некоторое целое число
Но тогда , а значит число не является простым. Значит такой случай невозможен
Если число р при делении на 3 дает остаток 2, то оно имеет вид
p=3k+2, где k - некоторое целое число
Но тогда , а значит число не является простым. Значит такой случай невозможен
Значит число р при делении на 3 дает остаток 0, а значит число р делится нацело на 3. Число р делится нацело на 3 и является простым, значит число р может равняться только числу 3.
При р=3: - простое, что и требовалось доказать.Доказано
Число р при делении на 3 может давать остатки 0,1 или 2.
Если число р при делении на 3 дает остаток 1, то оно имеет вид
p=3k+1, где k - некоторое целое число
Но тогда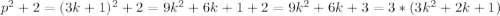
, а значит число 
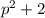не является простым. Значит такой случай невозможен
Если число р при делении на 3 дает остаток 2, то оно имеет вид
p=3k+2, где k - некоторое целое число
Но тогда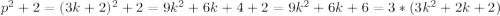
, а значит число 
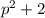не является простым. Значит такой случай невозможен
Значит число р при делении на 3 дает остаток 0, а значит число р делится нацело на 3. Число р делится нацело на 3 и является простым, значит число р может равняться только числу 3.
При р=3: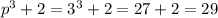
- простое, что и требовалось доказать.Доказано