Известно, что сумма квадратов последовательный натуральных чисел от 1 до n можно рассчитать по формуле S= 1/6*(2n + 1)*(n^2 + n). Пользуясь этой формулой, найди 2^2 + 3^2 + 4^2 + ... + 20^2.
Необходимо найти сумму квадратов натуральных чисел до n=20, однако данная формула учитывает ещё и , а в сумме, которую нужно найти, это слагаемое отсутствует, поэтому необходимо вычесть 1 из конечного результата
2869
Объяснение:
Необходимо найти сумму квадратов натуральных чисел до n=20, однако данная формула учитывает ещё и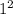 , а в сумме, которую нужно найти, это слагаемое отсутствует, поэтому необходимо вычесть 1 из конечного результата
, а в сумме, которую нужно найти, это слагаемое отсутствует, поэтому необходимо вычесть 1 из конечного результата
ответ: 2869
Объяснение: