Известны координаты двух противоположных вершин квадрата (вершины перечислены против часовой стрелки): (6; −6) и (−6; 6).
Определи координаты двух других вершин.
Сколько решений имеет задача?

Подробное объяснение: в задании номер 1 число 3 в 4 степени возводится в 5 степень. Когда ты видишь что-то наподобие этого, то степени перемножаются: то есть 4 степень умножаем на 5 степень и получаем 20 степень, то есть 3 в 20 степени. Далее, в числителе, видим:

Здесь степени тоже умножаюся, потому что умножаются сами числа. Перемножаем и получаем 3 в 23 степени. Ну и затем остается сократить то, что получилось:

Сокращаем и получаем:

Задание номер 2.

Ну, тут все просто, тут надо правильно перемножить, как на фото. С умножением степеней ситуация та же, что и в 1 задании.

Надеюсь

1. Область определения функции — множество всех действительных чисел.

2. Множество значений функции:

Так как синус изменяется от -1 до 1, то оценивая в виде двойного неравенства, имеем

Множество значений функции y=-2sinx: отрезок [-2;2].

3. Функция периодическая с периодом T = 2π

4. Функция нечетная , так как y(-x) = 2sin x = -y(x)

5. Наибольшее значение, равное 2, при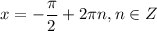

Наименьшее значение, равное -2, при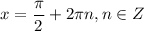

6. Функция возрастает на отрезке и на отрезках, получаемых сдвигами этого отрезка на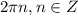

убывает на отрезке и на отрезках, получаемых сдвигами этого отрезка на