Чтобы графически решить систему уравнений надо выразить y через x и затем построить графики получившихся функций на одной координатной плоскости, их точки пересечения будут решениями данной системы. приводим к функциям: 1) y=-x^2+4 график - парабола, ветви вниз вершина: (0;4) найдем нули: y=0; x^2=4; x1=2; x2=-2 (2;0), (-2;0) Чтобы построить график этой функции, берем график y=-x^2 и сдвигаем его на 4 точки вверх по оси y, получим y=-x^2+4 и также этот график будет проходить через вышеуказанные точки. 2) y=x+2 линейная функция, для построения графика нужны 2 точки x=0; y=2; (0;2) y=0; x=-2; (-2;0) график в приложении: функция 1 - красным цветом, 2 - синим цветом они пересекаются в точках (-2;0) и (1;3) - это и есть решения системы. ответ: (-2;0), (1;3)
Графики вида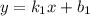
и 
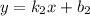параллельны, если выполняется условие 
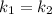при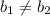 
Графики вида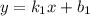
и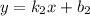 
пересекаются, если выполняется условие 
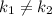при любых b
Графики вида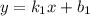
и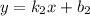 
совпадают, если выполняются условия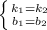 
Поэтому
1) y = 2x - 7
Параллельны: y = 2x
Пересекаются: y = x
Совпадают: y = 2x - 7
2) y = 3x + 1,4
Параллельны: y = 3x
Пересекаются: y = x
Совпадают: y = 3x + 1,4
3) y = x + 3,5
Параллельны: y = x
Пересекаются: y = 2x
Совпадают: y = x + 3,5
4) y = 3x - 10,5
Параллельны: y = 3x
Пересекаются: y = x
Совпадают: y = 3x - 10,5
5) y = 3x -7
Параллельны: y = 3x
Пересекаются: y = x
Совпадают: y = 3x - 7
приводим к функциям:
1) y=-x^2+4
график - парабола, ветви вниз
вершина:
(0;4)
найдем нули:
y=0; x^2=4; x1=2; x2=-2
(2;0), (-2;0)
Чтобы построить график этой функции, берем график y=-x^2 и сдвигаем его на 4 точки вверх по оси y, получим y=-x^2+4
и также этот график будет проходить через вышеуказанные точки.
2) y=x+2
линейная функция, для построения графика нужны 2 точки
x=0; y=2; (0;2)
y=0; x=-2; (-2;0)
график в приложении:
функция 1 - красным цветом, 2 - синим цветом
они пересекаются в точках (-2;0) и (1;3) - это и есть решения системы.
ответ: (-2;0), (1;3)