Пусть x - Обрабатываемая площадь посевов в день (ед. измерения - га/день), тогда по норме он должен выполнить заказ ровно за 52/x дней, но известно, что на предыдущий день (т.е на ), он обработал от 48 до 54,6 га, со скоростью, превышающей норму на 3 (т.е скорость равна x+3) итого получаем
поработаем сначала с выражением слева:
52/x - 1 = (52-x)/x, т.е. в Левых частях получается выражение (52-x)(x+3)/x
Раскроем скобки: (-x^2 + 49x + 156)/x
так как x > 0 (Действительно, механизатор не может обрабатывать в отрицательную площадь земли), то можем домножить на x (Обращу внимание, что домножать на x можно ТОЛЬКО если известно, что он только одного знака (в силу одз или условий задачи), причем если x всегда < 0, то нужно еще и поменять знак неравенства):
Нужно было сделать заказ за целое число дней, это означает что 52/x - целое число. Максимально возможное значение 52/x при x=10 52/10=5,2, Минимальное при x=13, 52/13 = 4 т.е. заказ выполнен при норме за 4 или 5 дней, если за 4, то скорость при норме 52/4 = 13 га в день, если за 5 дней, то 52/5 = 10,4 га в день
Виразіть з цієї формули швидкість тіла v.
10,4 или 13 га в день
Объяснение:
Пусть x - Обрабатываемая площадь посевов в день (ед. измерения - га/день), тогда по норме он должен выполнить заказ ровно за 52/x дней, но известно, что на предыдущий день (т.е на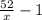
), он обработал от 48 до 54,6 га, со скоростью, превышающей норму на 3 (т.е скорость равна x+3) итого получаем
поработаем сначала с выражением слева:
52/x - 1 = (52-x)/x, т.е. в Левых частях получается выражение (52-x)(x+3)/x
Раскроем скобки: (-x^2 + 49x + 156)/x
так как x > 0 (Действительно, механизатор не может обрабатывать в отрицательную площадь земли), то можем домножить на x (Обращу внимание, что домножать на x можно ТОЛЬКО если известно, что он только одного знака (в силу одз или условий задачи), причем если x всегда < 0, то нужно еще и поменять знак неравенства):
Решим неравенства по отдельности:
1) -x^2 + x + 156 >= 0 2) -x^2-5,6 + 156 <= 0 |*5
D = 1 + 624 = 625 (25*25) -5x^2-28x+780 <= 0
x1 = (-1 - 25)/-2 = 13 D =784 + 15600=16384 (128*128)
x2 = (-1+25)/-2 = -12 x1 = (28-128)/-10 = 10
Далее используя метод x2 = (28+128)/-10 = -15,6
интервалов или свойства Далее используя метод
параболы получаем: интервалов или св-ва параболы:
-12 <= x <= 13 x <= -15,6 или x >= 10
x > 0, следовательно x > 0 следовательно
x <= 13 x >= 10
Нужно было сделать заказ за целое число дней, это означает что 52/x - целое число. Максимально возможное значение 52/x при x=10 52/10=5,2, Минимальное при x=13, 52/13 = 4 т.е. заказ выполнен при норме за 4 или 5 дней, если за 4, то скорость при норме 52/4 = 13 га в день, если за 5 дней, то 52/5 = 10,4 га в день
№ 1
Пусть х - количество мобильных пунктов управления.
(х² - х) : 2 = 36
х² - х = 36 * 2
х² - х = 72
х² - х - 72 = 0
D = (- 1)² - 4 * (-72) = 1 + 288 = 289 = 17²
Второй корень не подходит, значит, количество мобильных пунктов управления равно 9.
ответ: 9.
№ 2
Пусть х - % снижения стоимости товара в первый раз,
тогда 2х - % снижения стоимости товара во второй раз.
(50 - 50 : 100 * х) руб. - стоимость товара после первого снижения цены;
((50 - 50 : 100 * х) - (50 - 50 : 100 * х) : 100 * 2х) руб. - стоимость товара после второго снижения цены.
(50 - 50 : 100 * х) - (50 - 50 : 100 * х) : 100 * 2х = 29,75
50 - 0,5х - (50 - 0,5х) : 100 * 2х = 29,75
50 - 0,5х - х + 0,01х² = 29,75
0,01х² - 1,5х + 50 - 29,75 = 0
0,01х² - 1,5х + 20,25 = 0
х² - 150х + 2025 = 0
D = 150² - 4 * 2025 = 22500 - 8100 = 14400 = 120²
Первый корень не подходит, так как процент снижения не может быть больше 100%, значит, в первый раз цена товара снизилась на 15%.
ответ: 15%.