так как мы не можем определить нули производной, значит функция не имеет стационарных точек. Подставив любое значение из области определения функции( D(y): x є (4 ; ∞) ) мы увидим что , а это сведетельствует что она монотонно возростает на всем промежутке на котором определена
Объяснение:
Найдем прозводную функции f(x):
найдем нули производной
так как мы не можем определить нули производной, значит функция не имеет стационарных точек. Подставив любое значение из области определения функции( D(y): x є (4 ; ∞) ) мы увидим что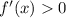 , а это сведетельствует что она монотонно возростает на всем промежутке на котором определена
, а это сведетельствует что она монотонно возростает на всем промежутке на котором определена