Пусть числитель дроби равен х, тогда знаменатель - (х+1). Если числитель и знаменатель дроби увеличить на 1: , то дробь увеличится на 1/12
Составим уравнение
По теореме Виета
x1 = -5
x2 = 2
5/4 - не соответствует условию.
Исходная дробь: 2/3.
2) Пусть скорость течения реки равна х км/ч, тогда скорость против течения равна (20-x) км/ч, а по течению (20+x) км/ч. Время движения против течения равно 20/(20-x) часов, а по течению - 20/(20+x) часов. На весь путь лодка затратила 2.5 - 25/60= 2.5-5/12 = 25/12 часов.
a)f(x)=(8x⁵-5x⁸)¹²
f ' (x) = ((8x⁵-5x⁸)¹²) ' = 12*(8x⁵-5x⁸)¹¹ * (8x⁵-5x⁸) ' = 12*(8x⁵-5x⁸)¹¹ * (40x⁴-40x⁷) = 12*(8x⁵-5x⁸)¹¹ * 40x⁴(1-x³) = 480x⁴ * (8x⁵-5x⁸)¹¹ * (1-x³)
б)f(X)=(1/9 - 3x³)²⁷
f ' (x) = ((1/9 - 3x³)²⁷) ' = 27(1/9 - 3x³)²⁶ * (1/9 - 3x³) ' = 27(1/9 - 3x³)²⁶ * (-3*3x²) = 27(1/9 - 3x³)²⁶ * (-9x²) = -243x² * (1/9 - 3x³)²⁶
в) f(x)=(4x¹⁰-5x)¹⁰
f ' (x) = ((4x¹⁰-5x)¹⁰) ' = 10(4x¹⁰-5x)⁹ * (4x¹⁰-5x) ' = 10(4x¹⁰-5x)⁹ * (40x⁹-5)= 10(4x¹⁰-5x)⁹ * 5(8x⁹-1)=50(4x¹⁰-5x)⁹ * (8x⁹-1)
г)f(x)=(x⁵-4x⁴)¹³⁰
f ' (x) = ((x⁵-4x⁴)¹³⁰) ' = 130(x⁵-4x⁴)¹²⁹ * (x⁵-4x⁴) ' = 130(x⁵-4x⁴)¹²⁹ * (5x⁴-16x³) = 130(x⁵-4x⁴)¹²⁹ * x³(5x-16) = 130*x³ * (x⁵-4x⁴)¹²⁹ * (5x-16)
Пусть числитель дроби равен х, тогда знаменатель - (х+1). Если числитель и знаменатель дроби увеличить на 1: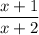
, то дробь увеличится на 1/12
Составим уравнение
По теореме Виета
x1 = -5
x2 = 2
5/4 - не соответствует условию.
Исходная дробь: 2/3.
2) Пусть скорость течения реки равна х км/ч, тогда скорость против течения равна (20-x) км/ч, а по течению (20+x) км/ч. Время движения против течения равно 20/(20-x) часов, а по течению - 20/(20+x) часов. На весь путь лодка затратила 2.5 - 25/60= 2.5-5/12 = 25/12 часов.
Составим уравнение:
Корень х=-4 не удовлетворяет условию.
ответ: скорость течения реки равна 4 км/ч.