Как расположены относительно друг друга графики функции (обосновать ответ): а)y=9x-5 и у=6+4х;
б)у=4х и y=4+6х;
в)у=3х-2 и y=-8+3x

Область определения находить очень просто. Проверяем, накладывается ли какое-либо граничение на функцию: если функция представляет собой дробь,то знаменатель не должен быть равен нулю; если в функции присутствует корень, то подкоренное выражение должно быть больше либо равно нулю; если в функции присутствует логарифм, то там ограничения согласно определению логарифма.

Затем, найдя область определения (какие значения может принимать х), смотрим, какие значения может принимать у на данной области определения. Это и будет множество значений функции 

1)  

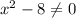
2)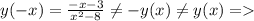 не является четной и нечетной

3)Горизонтальная:

y=0 - горизонтальная асимптота

Наклонная: y=kx+b

Наклонных нет

Вертикальная x = a, где а - точка разрыва

- вертикальные асимптоты

4)

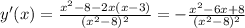
y' не сущ. при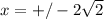  

y' = 0 при х=2; х=4

      -                 -               +        +            -

-----------0-----------------.-----0---------.----------->x

           -2sqrt(2)            2      2sqrt(2)  4 

x = 2 - точка min y(2) = 1/4 - наименьшее значение

x = 4 - точка max y(4) = 1/8 - наибольшее значение

 5)OX: y=0; x = 3 A(3;0)

OY: x=0; y=3/8 B(0;3/8)