Как узнать какие числа не являются членами арифметической прогрессии я где-то прочитала что что нецелые числа не являются членами арифметической прогрессии, это правда??
Если функция линейная, то можно объём определить без интеграла. График функции y=Ix-1I - это ломаная линия, идущая от точки (-1, 2) вниз до точки (1, 0) и вверх до (2,1) Если считать, что запись "Найдите объем тела, полученного при вращении вокруг оси абсцисс фигуры, ограниченной линией y=0" означает, что нужно определить только половину фигуры, то это будет половины двух конусов: - радиус основания большего конуса 2, высота - 2, - радиус основания меньшего конуса 1, высота - 1 V = S*H/3 = πR²H / 3 = π2²*2 /3 + π1²*1 / 3 = =8,3776+1,0472 = 9,4248. Если разделить на 2, получим 4,7124 куб. ед.
1) проверяем условие при наименьшем возможном значении n.
n>5, значит проверяем условие при n=6
Верно!
2) Сделаем предположение, что для всех n=k, k>5 верно неравенство:
3) Тогда при n=k+1 должно выполняться неравенство:
Вернемся к неравенству из второго пункта и домножим его на 2:
Подставим 2k² в 3-й пункт и рассмотрим полученное неравенство:
по методу интервалов определяем, что неравенство k²-2k-1>0 выполняется при k>1+√2, тогда при k>5 оно тоже выполняется (так как 5>1+√2)
Тогда обратным ходом получаем 2k²>k²+2k+1 при k>5 или 2k²>(k+1)² при k>5
Если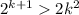
, а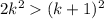 
, при k>5
То есть,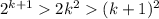
, при k>5, то по закону транзитивности:
График функции y=Ix-1I - это ломаная линия, идущая от точки (-1, 2) вниз до точки (1, 0) и вверх до (2,1)
Если считать, что запись "Найдите объем тела, полученного при вращении вокруг оси абсцисс фигуры, ограниченной линией y=0" означает, что нужно определить только половину фигуры, то это будет половины двух конусов:
- радиус основания большего конуса 2, высота - 2,
- радиус основания меньшего конуса 1, высота - 1
V = S*H/3 = πR²H / 3 = π2²*2 /3 + π1²*1 / 3 =
=8,3776+1,0472 = 9,4248.
Если разделить на 2, получим 4,7124 куб. ед.