2
Объяснение:
(у²-4у+4)/(у²-4) + (10у-у²)/(у²+2у)= при у=2
В числителе первой дроби развёрнут квадрат разности, свернуть, в знаменателе разность квадратов, развернуть.
В числителе второй дроби вынести у за скобки, в знаменателе вынести у за скобки:
=(у-2)²/(у-2)(у+2) + [у(10-у)]/[y(y+2)]=
общий знаменатель y(y+2)(у-2), надписываем над числителями дополнительные множители:
=[y(y-2)²+y(10-у)(у-2)] / [y(y+2)(у-2)]=
=y[(у²-4у+4)+(10-у)(у-2)] / y[(y+2)(у-2)]=
у сокращаем, раскрываем скобки:
=(у²-4у+4+10у-20-у²+2у)/[(y+2)(у-2)]=
приводим подобные члены в числителе:
=(8у-16)/[(y+2)(у-2)]=
=8(у-2)/[(y+2)(у-2)]=
сокращение (у-2) и (у-2) на (у-2):
=8/(у+2)= 8/(2+2)=8/4=2
1) x² + 2x - 3 = 0
D = b² - 4ac = 2² - 4 · 1 · (-3) = 4 + 12 = 16
Т.к. D > 0, то квадратное уравнение имеет два действительных корня:
x1 = = = = -3
x2 = = = = 1
ответ: -3 ; 1
2) 5x² - 6 = (6x - 5) (2x - 3)
5x² - 12х² + 18х + 10х - 15 - 6 = 0
7x² - 28x + 21 = 0
D = b² - 4ac = (-28)² - 4 · 7 · 21 = 784 - 588 = 196
x1 = = = = 1
x2 = = = = 3
ответ: 1 ; 3
Примечание: где â - это корень
2
Объяснение:
(у²-4у+4)/(у²-4) + (10у-у²)/(у²+2у)= при у=2
В числителе первой дроби развёрнут квадрат разности, свернуть, в знаменателе разность квадратов, развернуть.
В числителе второй дроби вынести у за скобки, в знаменателе вынести у за скобки:
=(у-2)²/(у-2)(у+2) + [у(10-у)]/[y(y+2)]=
общий знаменатель y(y+2)(у-2), надписываем над числителями дополнительные множители:
=[y(y-2)²+y(10-у)(у-2)] / [y(y+2)(у-2)]=
=y[(у²-4у+4)+(10-у)(у-2)] / y[(y+2)(у-2)]=
у сокращаем, раскрываем скобки:
=(у²-4у+4+10у-20-у²+2у)/[(y+2)(у-2)]=
приводим подобные члены в числителе:
=(8у-16)/[(y+2)(у-2)]=
=8(у-2)/[(y+2)(у-2)]=
сокращение (у-2) и (у-2) на (у-2):
=8/(у+2)= 8/(2+2)=8/4=2
1) x² + 2x - 3 = 0
D = b² - 4ac = 2² - 4 · 1 · (-3) = 4 + 12 = 16
Т.к. D > 0, то квадратное уравнение имеет два действительных корня:
x1 =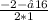 =
= 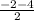 =
= 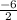 = -3
= -3
x2 =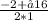 =
= 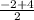 =
= 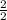 = 1
= 1
ответ: -3 ; 1
2) 5x² - 6 = (6x - 5) (2x - 3)
5x² - 12х² + 18х + 10х - 15 - 6 = 0
7x² - 28x + 21 = 0
D = b² - 4ac = (-28)² - 4 · 7 · 21 = 784 - 588 = 196
Т.к. D > 0, то квадратное уравнение имеет два действительных корня:
x1 =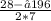 =
= 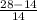 =
= 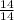 = 1
= 1
x2 =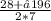 =
= 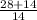 =
= 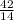 = 3
= 3
ответ: 1 ; 3
Примечание: где â - это корень