Т. к исходный график параллелен прямой у=3х-1 , значит, в исходной формуле к=3, так как график проходит через точку м(2; 1), то можно подставить в формулу у=кх+b вместо х и у значения 2 и 1 соответственно и k=3, получаем: 1=3*2+b 1=6+b b=-5 y=3x-5чертим систему координат, отмечаем положительные направления стрелками вправо и вверх, подписываем оси вправо - х, вверх -у. отмечаем начало координат - точка о и единичные отрезки по каждой оси в 1 клетку. графиком является прямая, для её построения достаточно двух точек, запишем их координаты в таблицу: х= 0 3 у= -5 1 ставим координаты в системе и проводим через них прямую линию. подписываем график у=3х-5.
Имеем квадратное уравнение, где с - некоторое произвольное число (параметр), поэтому при разных значениях с уравнение может как иметь корни, так и не иметь. Поэтому нужно решить уравнения для всех возможных значений с.
Найдем дискриминант:
Рассмотрим 3 различных случая:
1) D < 0. Если D < 0, то уравнение не имеет решений. Найдем значения с, при которых дискриминант отрицателен: 64 - 8c < 0; 8c > 64 ⇔ c > 8. При таких значениях с корней у нас не будет вообще.
2) D = 0. Если D = 0, то уравнение имеет единственное решение: Найдем значение с, при котором дискриминант равен 0: 64 - 8c = 8 ⇔ c = 8. При таком значении параметра имеем один корень - х = 2.
3) D > 0. Если D > 0, то уравнение имеет два различных корня, которые находятся по общей формуле: . Выразим каждый из корней:
Аналогично
Найдем значения с, при которых дискриминант положителен: 64 - 8с > 0; 8с < 64 ⇔ c < 8. При таких значениях параметра у нас будут два корня:
ОТВЕТ: если с < 8, то если с = 8, то х = 2; если с > 8, то корней нет.
Объяснение: 2x²-8x+c = 0.
Имеем квадратное уравнение, где с - некоторое произвольное число (параметр), поэтому при разных значениях с уравнение может как иметь корни, так и не иметь. Поэтому нужно решить уравнения для всех возможных значений с.
Найдем дискриминант: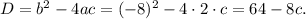
Рассмотрим 3 различных случая:
1) D < 0. Если D < 0, то уравнение не имеет решений. Найдем значения с, при которых дискриминант отрицателен: 64 - 8c < 0; 8c > 64 ⇔ c > 8. При таких значениях с корней у нас не будет вообще.
2) D = 0. Если D = 0, то уравнение имеет единственное решение: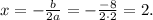
Найдем значение с, при котором дискриминант равен 0: 64 - 8c = 8 ⇔ c = 8. При таком значении параметра имеем один корень - х = 2.
3) D > 0. Если D > 0, то уравнение имеет два различных корня, которые находятся по общей формуле: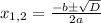
. Выразим каждый из корней:
Аналогично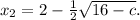
Найдем значения с, при которых дискриминант положителен: 64 - 8с > 0; 8с < 64 ⇔ c < 8. При таких значениях параметра у нас будут два корня: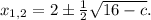
ОТВЕТ: если с < 8, то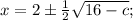
если с = 8, то х = 2; если с > 8, то корней нет.