(см. объяснение)
Объяснение:
В своем ответе я приведу два допустимых решения.
1:
Рассмотрим уравнение .
Пусть y - один из его корней.
Тогда по условию - второй корень уравнения.
Итого имеем систему:
Решив ее, получим, что .
Проверим теперь каждое значение параметра и выберем те, при которых выполняется решение задачи.
(здесь надо решить 4 уравнения при всех найденных значениях параметра; я этого делать не буду, так как эти действия долгие, но очевидные)
Итого получили, что при и один из корней уравнения является квадратом другого.
2:
Решим это уравнение через дискриминант:
Выразим корни уравнения:
По условию один из корней должен являться квадратом другого.
Тогда возможны два случая:
/или/
Но второй не будет иметь корней, так как .
Запишем единственное уравнение и найдем искомые значения параметра:
Меняем на :
Откуда или .
Обратная замена:
Или:
Итого имеем, что при и один из корней уравнения является квадратом другого.
Задание выполнено!
В решении.
Построение графика у = |x|:
y = {x, если x ≥ 0
−x, если x < 0.
1) Сначала построить прямую y = x и выделить её часть на луче [0; +∞).
2) Затем построить прямую y = −x и выделить её часть на открытом луче (−∞; 0).
3) Полученные лучи построить в одной системе координат; это и есть график функции y = |x|.
|x + 1| - смещение графика влево по оси Ох на 1 единицу;
|x + 1| + 1 - смещение графика вверх по оси Оу на 1 единицу.
График на рисунке соответствует уравнению у = |x + 1| + 1, ответ Б.
(см. объяснение)
Объяснение:
В своем ответе я приведу два допустимых решения.
1:
Рассмотрим уравнение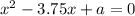
.
Пусть y - один из его корней.
Тогда по условию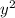
- второй корень уравнения.
Итого имеем систему:
Решив ее, получим, что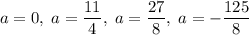
.
Проверим теперь каждое значение параметра и выберем те, при которых выполняется решение задачи.
(здесь надо решить 4 уравнения при всех найденных значениях параметра; я этого делать не буду, так как эти действия долгие, но очевидные)
Итого получили, что при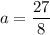
и 
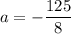один из корней уравнения 
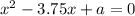является квадратом другого.
2:
Решим это уравнение через дискриминант:
Выразим корни уравнения:
По условию один из корней должен являться квадратом другого.
Тогда возможны два случая:
Но второй не будет иметь корней, так как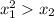
.
Запишем единственное уравнение и найдем искомые значения параметра:
Меняем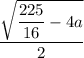
на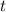 
:
Откуда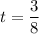
или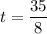 
.
Обратная замена:
Или:
Итого имеем, что пр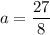и
и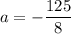 
один из корней уравнения 
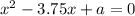является квадратом другого.
Задание выполнено!
В решении.
Объяснение:
Построение графика у = |x|:
y = {x, если x ≥ 0
−x, если x < 0.
1) Сначала построить прямую y = x и выделить её часть на луче [0; +∞).
2) Затем построить прямую y = −x и выделить её часть на открытом луче (−∞; 0).
3) Полученные лучи построить в одной системе координат; это и есть график функции y = |x|.
|x + 1| - смещение графика влево по оси Ох на 1 единицу;
|x + 1| + 1 - смещение графика вверх по оси Оу на 1 единицу.
График на рисунке соответствует уравнению у = |x + 1| + 1, ответ Б.