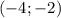1)
2)
3)
1) y=x²+10 - парабола , поднятая на 10 точек вверх, координаты вершины (0;10)
2) y=x²-5 - парабола, на 5 точек вниз, координаты вершины (0;-5)
3) y=(x+7)² - парабола, передвинутая на 7 точек влево, вершина (-7;0)
4) y=(x-8)²-парабола, передвинутая на 8 точек вправо, вершина (8;0)
4) y=x²
1) y=x²+5
2)y=x²-4
3)y=(x-3)²
4)y=(x+6)²
5)
На фото, c Ox пересекается график функции y=x²-4.
Точки пересечения с Ox (-2;0) и (2;0)
И y=x²-1
Точки пересечения с Ox (-1;0) и (1;0)
С Oy : y=x²-1, (0;-1)
y=x²+2,5 , (0;2,5)
y=x²-4, (0;-4)
y=x²+4,5, (0;4,5)
1.
Сложим:
Подставим во второе уравнение и получим:
<=>
Замена:
=>
Находим значения переменной , подставляя значения в :
при:
ответ:
1)
2)
3)
1) y=x²+10 - парабола , поднятая на 10 точек вверх, координаты вершины (0;10)
2) y=x²-5 - парабола, на 5 точек вниз, координаты вершины (0;-5)
3) y=(x+7)² - парабола, передвинутая на 7 точек влево, вершина (-7;0)
4) y=(x-8)²-парабола, передвинутая на 8 точек вправо, вершина (8;0)
4) y=x²
1) y=x²+5
2)y=x²-4
3)y=(x-3)²
4)y=(x+6)²
5)
На фото, c Ox пересекается график функции y=x²-4.
Точки пересечения с Ox (-2;0) и (2;0)
И y=x²-1
Точки пересечения с Ox (-1;0) и (1;0)
С Oy : y=x²-1, (0;-1)
y=x²+2,5 , (0;2,5)
y=x²-4, (0;-4)
y=x²+4,5, (0;4,5)
1.
Сложим:
Подставим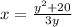 во второе уравнение
во второе уравнение 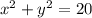 и получим:
и получим:
Замена:
Замена:
Находим значения переменной , подставляя значения
, подставляя значения  в
в 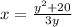 :
:
при:
ответ: