Всего в графе из вершин мы можем провести ребер. Но, конечно, некоторые (или даже все эти) ребра могут отсутствовать. То есть мы для каждого потенциального ребра делаем выбор: действительно включать его в граф или нет.
Таким образом, выбор из двух возможностей мы проводим раз. Значит, общее количество неориентированных графов с вершинами равно .
Эту формулу очень просто получить.
Всего в графе из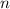 вершин мы можем провести
вершин мы можем провести 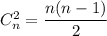 ребер. Но, конечно, некоторые (или даже все эти) ребра могут отсутствовать. То есть мы для каждого потенциального ребра делаем выбор: действительно включать его в граф или нет.
ребер. Но, конечно, некоторые (или даже все эти) ребра могут отсутствовать. То есть мы для каждого потенциального ребра делаем выбор: действительно включать его в граф или нет.
Таким образом, выбор из двух возможностей мы проводим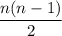 раз. Значит, общее количество неориентированных графов с
раз. Значит, общее количество неориентированных графов с 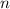 вершинами равно
вершинами равно 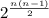 .
.