Контрольная работа №11 по теме: «Неравенства»
В а р и а н т 2
1. Решить линейные неравенства
1. 3x < –12;
2. 13 – 5x ≤ x – 5;
3. 6 – 6(x – 3) ≥ 2(x + 1) – 10.
2. Решить квадратные неравенства
1. x2 − 6x + 5 ≤ 0
2. 4x – x2 < 0;
3. x2 – 10x + 25 ≤ 0.
3. При каких значениях х имеет смысл выражение

Контрольная работа №11 по теме: «Неравенства»
В а р и а н т 1
1. Решить линейные неравенства
1. 6x > 72;
2. 4x – 6 > 6x + 14;
3. 3 – x ≤ 1 – 7(x + 1).
2. Решить квадратные неравенства
1. x2 – 2x – 35 > 0;
2. –x2 > − 16;
3. x2 – 2x > –1.
3. При каких значениях х имеет смысл выражение .

A(2 ; 4) 4=2^2 точка А принадлежит
B(3  ;6) 6<3^2 точка B не принадлежит
C(4 ; 8) 8<4^2 точка C не принадлежит
D(-3 ; 9) 9= (-3)^2 точка D принадлежит
R(0,5 ; 0,25) 0,25=0,5^2 точка R принадлежит  
S(1,2 ; 2,4) 2,4>1,2^2 точка S не принадлежит
E(1,5 ; 3) 3>1,5^2 точка Е не принадлежит
F(-2,5 ; 6,25) 6,25= (-2,5)^2 точка F принадлежит 
K(1\2 ; 1\4) 1/4=1/2^2 точка K принадлежит
P(2\3 ; 4\9) 4/9=2/3^2 точка P принадлежит
L(-5\7 ; 25\49) 25/49= (-5/7)^2 точка L принадлежит
M(-11\12 ; -121\144) -121/144< (-11/22)^2 точка M не принадлежит

Объяснение:

Посчитаем:

Тут выражение, равное разности степеней чисел 21 , 3 и 4

Свойство степени числа такое:

1.  если показатель (цифра сверху) положительное (больше нуля), то пишем обычную степень .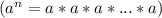

2.  если показатель равен нулю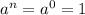

3.  если показатель меньше нуля, то пишем так: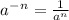

Рассмотрим на нашем примере и посчитаем:

1) 21 в 0 степени - 1 по второму свойству.

2) 3 в степени -2 равно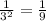 по 3 свойству.

3) 4 в степени -2 равно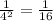 по 3 свойству.

А затем выполним над ними операции, приведя к общему знаменателю:

144, так как 144 делится и на 16, и на 9 , чтобы было удобнее считать.

- положительное число, то есть число. которое больше 0.  Что и требовалось доказать.