Контрольная работа №4 1. Найдите значение выражения – 8р
3 при р =
3
1
.
2. Выполните действия:
а) у
7
· у
14; б) у
19: у
5
; в) (у
2
)
7
; г) (2у)
5
.
3. Упростите выражение:
а) – 4х
5
у
2
· 3ху4
;
б) (3х
2
у
3
)
4
.
4. Постройте график функции у = х
2
. С графика
функции определите значение у при х = 3,5; х = – 2,5.
5. Вычислите:
2
6
81
3 27
.
6. Упростите выражение: а)
4
2 8 3
2
1
1
3
2
2
х у ху
;
б) (а
п+1)
3
: а
3п
.
Объяснение:
Мы докажем это равенство по индукции. Но сначала преобразуем правую часть равенства к более удобному для нас виду:
Теперь предположим что равенство верно для n=k:
Прибавив к обеим частям равенства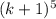 получим:
получим:
Займёмся преобразованием правой части этого равенства:
То есть если равенство верно для произвольного n=k, то оно также оказывается верным и для n=k+1. По индукции заключаем верность равенства для любого натурального n.
Если же вас интересует каким можно вывести формулу, которую мы только что доказали - напишите мне в ЛС.
Будем считать, что площадь равна 150 кв.ед.
Пусть один катет равен x, второй x + a, гипотенуза x + 2a.
При двух неизвестных надо составить 2 уравнения.
Первое по Пифагору.
x² + (x + a)² = (x + 2a)².
x² + x² + 2ax + a² = x² + 4ax + 4a².
x² - 2ax - 3a² = 0. D = 4a² - 4*1*3a² = 16a². √D = 4a.
x₁ = (2a - 4a)/2 = -a (отрицательное значение не принимаем).
x₂ = (2a + 4a)/2 = 3a.
Второе по площади: (1/2)*x*(x + a) = 150.
x² + ax = 300. Вместо х подставим 3a.
9a² + 3a² = 300.
12a² = 300, a² = 300/12 = 25, a = √25 = 5.
Отсюда находим стороны треугольника.
х = 3а = 3*5 = 15.
х + а = 15 + 5 = 20. Это катеты.
Гипотенуза равна 15 + 2*5 = 25.