КОНТРОЛЬНАЯ РАБОТА N 2 Вариант 1
1. Поетройте график линейной функции у = - ½x+1
С графика найдите:
а) наименьшее и наибольшее значення функции на от-
резке (-4; 6]:
б) значення переменной хпри которых у > 0.
2. Найдите координаты точки пересечения прямых у = 4.x
3. а) Найдите координаты точек пересечения графика ли-
нейного уравнення 4x - 3 + 12 = 0 с осями координ-
б) Определите, принадлежит ли графику данного уран-
нення точка D -0.
D(-0,5; 4).
4. а) Задайте линейную функцию у = kx формулой, если
известно, что ее график параллелен прямой -5де
б) Определите, возрастает или убывает заданная вами
линейная функция. .
5. При каком значенних р решение уравнения
рх - Зру б = 0
является пара чисел (1,5; -1,5)?​

Объяснение:

Построить график линейного уравнения:

1) 1,2у= -4,8

у= -4,8/1,2

у= -4

График - прямая линия, параллельна оси Ох и проходит

через точку у= -4

2)1,5у=6

у=6/1,5

у=4

График - прямая линия, параллельна оси Ох и проходит

через точку у=4

Построить график линейного уравнения с двумя переменными:

3)х+у=5

4)у-4х=0

Построить графики. Графики линейной функции, прямые линии. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.  

Прежде нужно преобразовать уравнения в более удобный для вычислений вид:  

              х+у=5                                            у-4х=0

              у=5-х                                             у=4х

                                     Таблицы:

        х    -1      0      1                                 х     -1      0      1

        у     6      5     4                                 у    -4      0     4

используем теорему  Виета для решения всех заданий. Напомню, что по теореме Виета x1 + x2 = -p и x1 × x2 = q, где p и q коэффиценты уравнения x² + px + q = 0.

1. a) если корни равны 2 и 5, то p и q равны соответственно -7 и 10, подставляем их в исходное уравнение:

x² - 7x + 10 = 0, делаем все аналогично для пунктов б) и в):

б) x² - 2x -3 = 0

в) x² - 2,9x + 1 = 0

2. Подбором находим корни уравнений, затем делаем проверку:

а) 3; 2        3 × 2 = 6 и 3 + 2 = -(-5)

б) -3; -5     -3 × -5 = 15 и -3 - 5 = -8

в) 9; -1

г) 5; -2

д) 3; 14

е) 16; -5

3. Т.к. нам дан один корень, то можно найти второй через коэффицент q, а потом сделать проверку через коэффицент p:

a) 2 × x = -38, отсюда x = -19

проверим: -19 + 2 = -17, значит все правильно

б) поскольку это уравнение не приведенное, то разделим его на 7, чтобы сделать приведенным:

x² -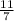 - = 0

теперь мы можем сделать тоже, что и в пункте а):

2 × x =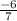, отсюда х =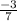

проверим: 2 - =

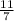
Все верно, значит мы решили правильно!