Костя и саша побежали наперегонки в магазин за лимонадом. у кости скорость больше, чем у саши на 1м/с. но в магазин мальчики ворвались одновременно – через 96 сек. произошло это потому, что по дороге саша упал только один раз, а костя целых четыре, а на падение требовалось 6 сек.: упасть, подняться и отряхнуться. какое расстояние нужно было преодолеть мальчикам до магазина?
y=1+x3, х∈(-∞;+∞) или D=(-∞;+∞)
y=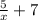
, х∈(-∞;0)∪(0;+∞) или D=(-∞;0)∪(0;+∞)
Объяснение:
Область определения функции - откуда до куда твой график существует по оси Х.
а) y=1+x3 график прямой х∈(-∞;+∞)
б) y=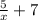
график гиберболы х∈(-∞;0)∪(0;+∞)
Если функция имеет вид: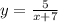
то х∈(-∞;-7)∪(-7;+∞)
Знаменатель х+7 говорит о том, что асимптота сдвинута по оси х влево.
Можно записывать ответ по разному, два варианта записи ответа, необходимо выбрать 1:
y=1+x3, (1вариант) х∈(-∞;+∞) или (2 вариант) D=(-∞;+∞)
y=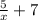
, (1вариант) х∈(-∞;0)∪(0;+∞) или (2 вариант) D=(-∞;0)∪(0;+∞)
Объяснение:
Имеется два существенно различных задания множеств. Можно либо перечислить все элементы множества, либо указать правило для определения того, принадлежит или не принадлежит рассматриваемому множеству любой данный объект.
Два множества A и B называются равными, если они состоят из одних и тех же элементов, т. е. если каждый элемент множества A принадлежит B и, обратно, каждый элемент B принадлежит A. Тогда пишут A = B.
Пустое множество — множество, не содержащее ни одного элемента. Одноэлементное множество — множество, состоящее из одного элемента. Универсальное множество (универсум) — множество, содержащее все мыслимые объекты.
Пересечением двух множеств, называется третье множество, сформированное из элементов, которые входят в оба первых множества.
Объединением двух множеств A и B называется множество A B, состоящее из тех и только тех элементов, которые принадлежат хотя бы одному из множеств A или B. Пересечением множеств A и B называется множество A B, которое состоит из тех и только тех элементов, которые принадлежат как множеству A, так и множеству B.