Кожному одноцифровому натуральному числу поставили у відповідність число, яке дорівнює потроєній остачі при ділкні цього числа на 2. Задайте цю функцію за до таблиці
Теорема 1 (первый признак равенства — по двум катетам)
Если катеты одного треугольника соответственно равны катетам другого треугольника, то такие прямоугольные треугольники равны.
Теорема 2 (второй признак равенства — по катету и прилежащему острому углу)
Если катет и прилежащий острый угол одного треугольника соответственно равны катету и прилежащему острому углу другого треугольника, то такие прямоугольные треугольники равны.
Теорема 3 (третий признак равенства — по гипотенузе и острому углу)
Если гипотенуза и острый угол одного треугольника соответственно равны гипотенузе и острому углу другого треугольника, то такие прямоугольные треугольники равны.
Теорема 4 (четвёртый признак равенства — по гипотенузе и катету)
Если гипотенуза и катет одного треугольника соответственно равны гипотенузе и катету другого треугольника, то такие прямоугольные треугольники равны.
4
Объяснение:
Теорема 1 (первый признак равенства — по двум катетам)
Если катеты одного треугольника соответственно равны катетам другого треугольника, то такие прямоугольные треугольники равны.
Теорема 2 (второй признак равенства — по катету и прилежащему острому углу)
Если катет и прилежащий острый угол одного треугольника соответственно равны катету и прилежащему острому углу другого треугольника, то такие прямоугольные треугольники равны.
Теорема 3 (третий признак равенства — по гипотенузе и острому углу)
Если гипотенуза и острый угол одного треугольника соответственно равны гипотенузе и острому углу другого треугольника, то такие прямоугольные треугольники равны.
Теорема 4 (четвёртый признак равенства — по гипотенузе и катету)
Если гипотенуза и катет одного треугольника соответственно равны гипотенузе и катету другого треугольника, то такие прямоугольные треугольники равны.
#1.
Пусть первое число - x; а второе число - y. Получим два уравнения:
Выразим x через y и подставим это значение в первое уравнение:
По теореме Виета:
Так как мы знаем, что оба числа положительные, то y = 13
Найдем x:
ответ: 12, 25.
#2.
Периметр - это сумма всех сторон; формула -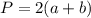
Найдем сумму длины и ширины:
Отсюда можно выразить длину b:
Диагонали в прямоугольнике образуют два равных прямоугольных треугольника, где диагонали - гипотенузы, а стороны - катеты.
Найдем длину одной диагонали:
По теореме Пифагора:
По теореме Виета:
Если a = 25, то b = 60, и наоборот. Длины сторон - 25 и 60 см.
ответ: 25, 60.