Сначала строим график , затем сдвигаем его на 1 единицу влево вдоль оси ОХ, получаем график функции . А потом отображаем ту часть графика, которая лежит ниже оси ОХ , в верхнюю полуплоскость и получим график заданной функции .
Как видно из графика . См. рис.
Сначала строим график , затем отображаем ту часть графика, которая лежит ниже оси ОХ , в верхнюю полуплоскость и получим график функции . Потом смещаем этот график на 6 единиц вверх вдоль оси ОУ , получим график заданной функции .
1) Каноническое уравнение параболы ее фокус находится в точке с координатами Координата точки находиться в системе уравнения Если уравнение касательной равна с учетом того что она проходит через точку получаем , подставляя
То есть касательная будет иметь вид Положим что перпендикуляр к касательной имеет вид он проходит через точку По условию расстояние от точки с координатами Координата точки Значит парабола имеет вид 2) центр окружности (так как центр лежит на оси ) Получаем систему уравнения Которая должна иметь одно решение, получаем Получаем уравнение окружности
Сначала строим график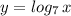 , затем сдвигаем его на 1 единицу влево вдоль оси ОХ, получаем график функции
, затем сдвигаем его на 1 единицу влево вдоль оси ОХ, получаем график функции 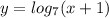 . А потом отображаем ту часть графика, которая лежит ниже оси ОХ , в верхнюю полуплоскость и получим график заданной функции
. А потом отображаем ту часть графика, которая лежит ниже оси ОХ , в верхнюю полуплоскость и получим график заданной функции 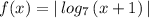 .
.
Как видно из графика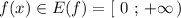 . См. рис.
. См. рис.
Сначала строим график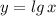 , затем отображаем ту часть графика, которая лежит ниже оси ОХ , в верхнюю полуплоскость и получим график функции
, затем отображаем ту часть графика, которая лежит ниже оси ОХ , в верхнюю полуплоскость и получим график функции 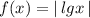 . Потом смещаем этот график на 6 единиц вверх вдоль оси ОУ , получим график заданной функции .
. Потом смещаем этот график на 6 единиц вверх вдоль оси ОУ , получим график заданной функции .
Как видно из графика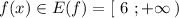 . См. рис.
. См. рис.
Каноническое уравнение параболы
Координата точки
То есть касательная будет иметь вид
Положим что перпендикуляр к касательной имеет вид
По условию расстояние от точки с координатами
Координата точки
Значит парабола имеет вид
2)
Получаем систему уравнения
Которая должна иметь одно решение, получаем
Получаем уравнение окружности