Найдем решения неравенства Ix-5I≤2; -2≤х-6≤2; 4≤х≤8- отрезок длиной 4
Найдем решения неравенства Ix-6I≥1
x-6≥1; х≥7 или х-6≤-1; х≤5; т.е. х∈(-∞;5]∪[7;8]
Из отрезка [4;8] выпадает только отрезок[5;7] длины 2
Используя геометрическое определение вероятности, найдем искомую вероятность, длина решений второго неравенства, которое находится в первом, составляет 2, это сумма длин отрезков [4;5] и [7;8], т.е. число благоприятствующих исходов равно 2, а общее число исходов 4, значит, вероятность равна 2/4=0.5
Найдем решения неравенства Ix-5I≤2; -2≤х-6≤2; 4≤х≤8- отрезок длиной 4
Найдем решения неравенства Ix-6I≥1
x-6≥1; х≥7 или х-6≤-1; х≤5; т.е. х∈(-∞;5]∪[7;8]
Из отрезка [4;8] выпадает только отрезок[5;7] длины 2
Используя геометрическое определение вероятности, найдем искомую вероятность, длина решений второго неравенства, которое находится в первом, составляет 2, это сумма длин отрезков [4;5] и [7;8], т.е. число благоприятствующих исходов равно 2, а общее число исходов 4, значит, вероятность равна 2/4=0.5
Решением является перебор вариантов:
Можно достать шары из урны четырьмя
1) 2 белых
2) 2 чёрных
3) 1 белый и 1 чёрный
4) сначала 1 чёрный, потом 1 белый.
Вероятности этих событий:
1)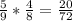
2)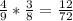
3)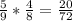
4)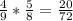
Вероятность того, что мы достанем из урны два одинаковых по цвету шара равна сумме вероятностей в первом и во втором случаях:
Вероятность вынимания шаров разных цветов (не важно в какой последовательности) равна сумме вероятностей в третьем и в четвёртом случаях:
Сравнивая две полученные дроби мы приходим к выводу, что вынуть два разных по цвету шара более вероятнее, чем два одинаковых.