Кто и сделает,всё правильно оставлю лучший ответ​

y=x^2-3x+2

1) Находим точки пересечения графика функции с осью Ох:

     х^2-3x+2=0

     x1=1, x2=2

    (1;0) и (2;0) - искомые точки

2) Находим уравнение касательной к графику функции в точке х=1

    y`(x)=(x^2-3x+2)`=2x-3

    y`(1)=2*1-3=-1   k1=-1

    y(1)=1^2-3*1+2=1-3+2=0

    y=0+(-1)(x-1)=-x+1 -уравнение касательной в точке х=1

3) Находим уравнение касательной к графику функции в точке х=2

    y`(2)=2*2-3=4-3=1  k2=1

    y(2)=2^2-3*2+2=4-6+2=0

    y=0+1(x-2)=x-2 -уравнение касательной в точке х=2

4) Коэффициент угла наклона первой касательной k1=-1, а второй касательной k2=1,

    следовательно, касательные взаимно перпендикулярны,

    т.е.угол между ними равен 90 градусов.

1) не является; 2) не является

Объяснение:

1) Является ли у функцией х, если у - это число десятых в десятичной записи числа х?

У некоторых чисел существует 2 формы десятичной записи: с 0 и с 9 в периоде.

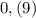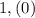Например, для числа 1 существуют 2 формы: и . В первом случае число десятых равно девяти, а во втором - нулю. То есть существует значение переменной 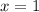, которому соответствуют несколько значений .

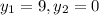Значит, у не является функцией х.

2) Является ли x функцией y, если у - это число десятых в десятичной записи числа х?

Рассмотрим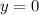 . Но число десятых у чисел 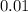и 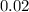равно нулю. То есть существует значение переменной 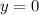, которому соответствуют несколько значений (например, ).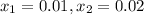

Значит, x не является функцией y.