При возведении 1 в степень, последняя цифра цифра всегда равна 1, и, если показатель степени делится на 4 с остатком 1, то последняя цифра числа равна последней цифре основания степению
14^2020 => 2020/4=505(ост.0)
Если, показатель степени делится на 4 без остатка, то, если основание степени - четное число, 14 - четное число, то последняя цифра равна 6.
13^2019 => 2019/4=504(ост.3)
Если остаток равен 3, то последняя цифра степени будет равна последней цифре в записи куба основания.
Последние цифры степеней чисел 3, 13, 23, ..., ...3 будут совпадать, поэтому в куб можно возвести только последнюю цифру основания:
(см. объяснение)
Объяснение:
Наименьшее значение, которое может принимать левая часть рано 8.
Наибольшее значение, которое может принимать правая часть равно 8.
Значит исходное равенство становится верным, если имеем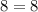 .
.
Тогда перейдем к системе уравнений:
Понятно, что вторая ее строчка решается несложно:
Поработаем теперь с первой:
Введем замену вида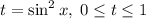 .
.
Тогда уравнение выше можно переписать:
Один из корней очевиден и равен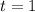 .
.
Понятно, что при уравнение
уравнение  не имеет корней.
не имеет корней.
Выполним теперь обратную замену:
Тогда ответом будет:
Задание выполнено!
ответ: 0
Объяснение:
11^2021+14^2020-13^2019
11^2021 => 2021/4=505(ост.1)
При возведении 1 в степень, последняя цифра цифра всегда равна 1, и, если показатель степени делится на 4 с остатком 1, то последняя цифра числа равна последней цифре основания степению
14^2020 => 2020/4=505(ост.0)
Если, показатель степени делится на 4 без остатка, то, если основание степени - четное число, 14 - четное число, то последняя цифра равна 6.
13^2019 => 2019/4=504(ост.3)
Если остаток равен 3, то последняя цифра степени будет равна последней цифре в записи куба основания.
Последние цифры степеней чисел 3, 13, 23, ..., ...3 будут совпадать, поэтому в куб можно возвести только последнюю цифру основания:
3^3=27 - последняя цифра числа равна 7.
11^2021+14^2020-13^2019= ...1 + ...6 - ..7 = ...0 (1+6-7=0)