Рассмотрим первый случай:
Если , то есть если или , то:
1) если и , то получаем верное равенство: , тогда — любое число;
2) если и , то получаем неверное равенство: , тогда уравнение не будет иметь решений;
3) если и , то получаем верное равенство: , тогда — любое число;
4) если и , то получаем неверное равенство: , тогда уравнение не будет иметь решений;
Рассмотрим второй случай:
Если , то есть если и , то
Объяснение:
Пусть скорость лодок в стоячей воде х км\ч,
тогда скорость лодки по течению ( х+4) км\ч,
а скорость лодки против течения (х-4) км\ч.
За 1,6 ч лодка по течению х+4) (км),
а лодка против течения х-4) (км),
вместе они х+4) +1,6*(х-4) или 92,8 км.
Составим уравнение
1,6*(х+4) +1,6*(х-4) = 92,8
1,6(х+4+х-4)=92,8
2х=92,8:1,6
2х=58
х=29 (это скорость лодек в стоячей воде в км\ч)
1,6*(29+4)=1,6*33=52,8 (км) до места встречи пройдёт лодка, плывущая по течению.
1,6*(29-4)=1,6*25=40 (км) до места встречи пройдёт лодка, плывущая против течения.
Рассмотрим первый случай:
Если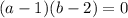
, то есть если 
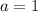или 
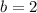, то:
1) если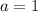
и 
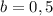, то получаем верное равенство: 
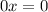, тогда 
— любое число;
2) если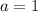
и 
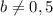, то получаем неверное равенство: 
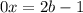, тогда уравнение не будет иметь решений;
3) если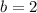
и 
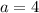, то получаем верное равенство: 
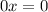, тогда 
— любое число;
4) если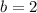
и 
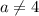, то получаем неверное равенство: 
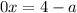, тогда уравнение не будет иметь решений;
Рассмотрим второй случай:
Если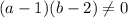
, то есть если 
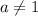и 
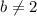, то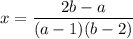 
еслиОбъяснение:
Пусть скорость лодок в стоячей воде х км\ч,
тогда скорость лодки по течению ( х+4) км\ч,
а скорость лодки против течения (х-4) км\ч.
За 1,6 ч лодка по течению х+4) (км),
а лодка против течения х-4) (км),
вместе они х+4) +1,6*(х-4) или 92,8 км.
Составим уравнение
1,6*(х+4) +1,6*(х-4) = 92,8
1,6(х+4+х-4)=92,8
2х=92,8:1,6
2х=58
х=29 (это скорость лодек в стоячей воде в км\ч)
1,6*(29+4)=1,6*33=52,8 (км) до места встречи пройдёт лодка, плывущая по течению.
1,6*(29-4)=1,6*25=40 (км) до места встречи пройдёт лодка, плывущая против течения.