1) Прямая пропорциональность у=кх, подставим значения х и у заданной точки -5=к*3, отсюда к=-5/3=-1 2/3, и функция у=-1 2/3*х 2) В точке пересечения с осью координата другой оси =0 а) с оью 0х у=0, тогда 0=1.2х-24, 1.2х=24, х=20; с осью 0у х=0, у=-24 б) 0х: у=0, 0=-3/5х+2, х=10/3=3 1/3; ось 0у х=0, у=2 в) график у=10 не зависит от х, т.е. для любого х прямая параллельна 0х и ее не пересекает, а пересекает только у=10 3) раз график параллелен оси 0х, то функция не зависит от х (см. пример 2), и имеет вид у=в, для заданной точки М(-3;1) у=1, значит в=1 и функция имеет вид у=1 для любого х, в том числе х=-3
За властивістю геом. прогресії кожен член є середнім геометричним двох сусідніх членів:
Використаємо формулу :
Перший варіант нам підходить. Тоді матимемо стаціонарну арифметична прогресію 12, 12, 12, 12... Стаціонарна арифметична прогресія одночасно є стаціонарною геометричною прогресією.
Другий варіант:
До речі, перевіримо:
Бачимо, що та справді утворюють геометричну прогресію {12; 24; 48} зі знаменником 2.
1) Прямая пропорциональность у=кх, подставим значения х и у заданной точки -5=к*3, отсюда к=-5/3=-1 2/3, и функция у=-1 2/3*х
2) В точке пересечения с осью координата другой оси =0
а) с оью 0х у=0, тогда 0=1.2х-24, 1.2х=24, х=20; с осью 0у х=0, у=-24
б) 0х: у=0, 0=-3/5х+2, х=10/3=3 1/3; ось 0у х=0, у=2
в) график у=10 не зависит от х, т.е. для любого х прямая параллельна 0х и ее не пересекает, а пересекает только у=10
3) раз график параллелен оси 0х, то функция не зависит от х (см. пример 2), и имеет вид у=в, для заданной точки М(-3;1) у=1, значит в=1 и функция имеет вид у=1 для любого х, в том числе х=-3
За властивістю геом. прогресії кожен член є середнім геометричним двох сусідніх членів:
Використаємо формулу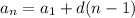
:
Перший варіант нам підходить. Тоді матимемо стаціонарну арифметична прогресію 12, 12, 12, 12... Стаціонарна арифметична прогресія одночасно є стаціонарною геометричною прогресією.
Другий варіант:
До речі, перевіримо:
Бачимо, що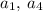
та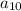 
справді утворюють геометричну прогресію {12; 24; 48} зі знаменником 2.
Відповідь. Умові задовольняють дві прогресії:
1) 12, 12, 12, 12, 12, 12.
2) 12, 16, 20, 24, 28, 32.