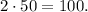По условию, г картона уходит на изготовление маленького пакета, а г картона — на изготовление большого. Также известно, что на изготовление маленьких пакетов и больших ушло г картона.
Получается, что
2)
Упростим и решим квадратное уравнение:
По теореме Виета (данное уравнение уже приведено, то есть коэффициент при равен единице, так что теорему можно применить напрямую),
Если равен , а — , то истинны оба равенства система уравнений, то есть эта пара чисел является решением системы уравнений. А по теореме Виета эта пара чисел ещё и является решением исходного квадратного уравнения.
Получается, что решением уравнения будут являться числа и . Однако по условию задачи первое число не подойдёт, ибо масса не может быть отрицательной, как и количество предметов. Получается, что масса маленького пакета, а также количество произведённых маленьких пакетов равно .
3)
На большой пакет по условию затрачивается в два раза больше картона, чем на маленький, то есть масса большого пакета будет равна
1)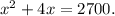
2)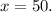
3)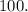
Объяснение:
1)
По условию, г картона уходит на изготовление маленького пакета, а
г картона уходит на изготовление маленького пакета, а 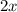 г картона — на изготовление большого. Также известно, что на изготовление
г картона — на изготовление большого. Также известно, что на изготовление  маленьких пакетов и
маленьких пакетов и 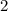 больших ушло
больших ушло 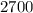 г картона.
г картона.
Получается, что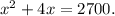
2)
Упростим и решим квадратное уравнение:
По теореме Виета (данное уравнение уже приведено, то есть коэффициент при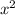 равен единице, так что теорему можно применить напрямую),
равен единице, так что теорему можно применить напрямую),
Если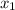 равен
равен 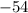 , а
, а 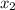 —
— 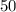 , то истинны оба равенства система уравнений, то есть эта пара чисел является решением системы уравнений. А по теореме Виета эта пара чисел ещё и является решением исходного квадратного уравнения.
, то истинны оба равенства система уравнений, то есть эта пара чисел является решением системы уравнений. А по теореме Виета эта пара чисел ещё и является решением исходного квадратного уравнения.
Получается, что решением уравнения будут являться числа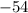 и
и 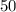 . Однако по условию задачи первое число не подойдёт, ибо масса не может быть отрицательной, как и количество предметов. Получается, что масса маленького пакета, а также количество произведённых маленьких пакетов равно
. Однако по условию задачи первое число не подойдёт, ибо масса не может быть отрицательной, как и количество предметов. Получается, что масса маленького пакета, а также количество произведённых маленьких пакетов равно 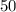 .
.
3)
На большой пакет по условию затрачивается в два раза больше картона, чем на маленький, то есть масса большого пакета будет равна