Квадратичная функция вида y=ax²+bx+c при a≠0 , ее график и свойства. Урок 2 Сопоставь уравнение квадратичной функции с осью симметрии ее графика – параболы. Количество соединений: 6 y = 4x2 – 24x + 5 y = 4x2 + 24x – 5 y = 0,5x2 – 5x + 3 y = –0,5x2 – 5x – 3 y = –2x2 – 8x – 3 y = -1/3x^2+1/3x-3 это ответы: x = 5 x = –5 x = 3 x = –3 x = 2 x = –2
(x+2)(3-x)=0
-x²+x+6=0
x²-x-6=0 D=26
x₁=3 x₂=-2
S=∫³₋₂(-x₂+x+6)dx=(-x³/3+x²/2+6x) |³₋₂=
-3³/3+3²/2+6*3-((-2)³/3+(-2)²/2+6*(-2))=-9+4¹/₂+18-(8/3+2-12)=
=13¹/₂-(-7¹/₃)=20⁵/₆≈20,8(3) (кв. ед.).
2) y=9-x² y=7-x y=0 s-?
9-x²=7-x
x²-x-2=0 D=9
x₁=2 x₂=-1
9-x²=0
x²=9
x₁=-3 x₂=3
7-x=0
x=7 ⇒
Обшая площадь состоит из четырёх площадей:
9-x² 7-x 9-x² 0
-3-1237
S=∫⁻¹₋₃(9-x²)dx+∫²₋₁(7-x)dx+∫³₂(9-x²)dx+∫⁷₃ (0)dx=
=(9x-x³/3) |⁻¹₋₃+(7x-x²/2) |²₋₁+(9x-x³/3) |³₂=
=(-9+1/3+27-9)+(14-2+7+1/2)+(27-9-18+8/3)=9¹/₃+19¹/₂+2²/₃=31¹/₂.
3) x=1
Объяснение:
3)
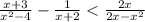ОЗД: x≠0, x≠2, x≠-2
Методом интервалов находим знаки выражения:
- + - +
-----------------°-------------°----------°---------------------->
-∞ -4.5 -2 2 +∞
Подходят интервалы, где стоит минус. Знак неравенства строгий - значит сами точки не берем. + добавляем ОДЗ. Получаем
x∈( -∞;-4.5)∪(-2;0)∪(0;2) - нужно целое неотрицательное значение x=1
5) x³-8x√x+18>0
(x√x)²-2*4*x√x+4²+2>0
(x√x-4)²+2>0
Квадрат (x√x-4)² - при любых неотрицательных x является неотрицательным числом - в нему добавляют 2 - значит получают строго положительное число . Доказали :)