Квадратные уравнения №4

Во Решите уравнеие -2х^2+50=0

1. 5 2. -5 3. 5;-5 4. корней нет

ответ:

Во Решите уравнение 3х^2+12=0

1. 2

2. -2

3. -4;4

4. -2;2

5. корней нет

ответ:

Во Найти наибольший корень уравнения 4х^2+10х+6=0

1. -1

2. -1,5

3. 1

4. 1,5

5. -3

6. -4

7. 3

8. 4

ответ:

Во Решите уравнение 25х^2+10х+1=0

1. 0,4

2. -0,4

3. 0,2

4. -0,2

ответ:

Во Сколько корней имеет уравнение 4х^2+30х+90=0

1. 2

2. нет корней

3. 0

ответ:

Во При каких значениях параметра р уравнение имеет 1 корень х^2+p*х+16=0

1. 4

2. -4

3. 8

4. -8;8

5. 8

6. -4;4

ответ:

Показать ответ

Ответ:

dianabiran

02.04.2020 10:32

1) Множество точек, удовлетворяющих неравенству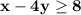 $\bf x-4y\geq 8$ ,

$\bf 4y\leq x-8\ \ ,\ \ y\leq \dfrac{x}{4}-2$ , лежат ниже прямой $\bf y=\dfrac{x}{4}-2$ .

Множество точек, удовлетворяющих неравенству $\bf (x-1)^2+y^2\leq 4$

лежат внутри окружности с центром в точке ( 1 : 0) , радиуса R=2 .

2) Множество решений системы неравенств изображено на рисунке.

Область заштрихована . Это полоса между прямыми х= -2 и х=2 , расположенная выше прямой у=3 . Сами прямые в область не входят, так как неравенства имеют строгие знаки .

$\left\{\begin{array}{l}\bf |\, x\, | < 2\\\bf y 3\end{array}\right\ \ \left\{\begin{array}{l}\bf -2 < x < 2\\\bf y 3\end{array}\right$

3) Фигура, изображённая на рисунке, может быть задана с системы неравенств $\left\{\begin{array}{l}\bf y\leq 4\ ,\\\bf y\geq x^2\end{array}\right$ .

Неравенство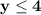 $\bf y\leq 4$ описывает множество точек, лежащих ниже прямой у=4 .

Неравенство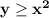 $\bf y\geq x^2$ описывает множество точек, расположенных внутри параболы 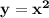$\bf y=x^2$ . Это можно определить, если рассматривать точку , которая находится внутри параболы , например, точка (1;2) , и точку с той же абсциссой х=1 , лежащую на параболе, имеющую ординату у=1²=1 . Сравним ординаты этих точек: 2>1 . Значит ординаты точек, находящихся внутри параболы, больше , чем ординаты точек, лежащих на параболе . Отсюда и получаем у≥х² .