Для того чтобы показать, что число является составным достаточно показать, что оно у него есть делители помимо 1 и самого себя. Для начала надо понять на какое число заканчивается . Для этого нужно понять на какую цифру заканчиваются степени двойки:
Таким образом последняя цифра в степенях двойки может быть только из множества {2, 4, 8, 6}, которое будет циклически повторяться. Дальше надо понять остаток от деления 1234 на 4. 1234 : 4 = 308 и остаток 2. Значит последния цифра у нас совершит 308 полных циклов и еще 2 шага. Таким образом число заканчивается на цифру 4. Следовательно заканчивается на цифру 5, а значит это число делится на 5 и как факт является составным.
Y(x)=x²+4, х₀=1, k=4 угловой коэффициент касательной к функции равен значению производной функции в точке касания, т.е. k=y'(x₀) 1) найдем производную: y'(x)=(x²+4)'=2x k=y'(x₀)=y'(1)=2*1=2 - угловой коэффициент касательной к графику функции в точке с абсциссой x₀=1 2) теперь известен угловой коэффициент k=4, но неизвестна точка касания x₀, т.е. y'(x₀)=k 2*x₀=4 x₀=2 чтобы найти ординату точки, подставим x₀ в функцию y(x): y₀=y(x₀)=2²+4=4+4=8 (2;4) - координаты точки, в которой угловой коэффициент касания равен k=4 3) уравнение касательной в общем виде: f(x)=y(x₀)+y'(x₀)*(x-x₀) x₀=1, y'(x₀)=2 - найдено выше под 1) y(x₀)=1²+4=5 подставляем найденные значения в общий вид: f(x)=5+2(x-1)=5+2x-2=2x+3 - уравнение касательной к графику функции в точке с абсциссой x₀=1
Объяснение:
Для того чтобы показать, что число является составным достаточно показать, что оно у него есть делители помимо 1 и самого себя. Для начала надо понять на какое число заканчивается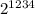
. Для этого нужно понять на какую цифру заканчиваются степени двойки:
Таким образом последняя цифра в степенях двойки может быть только из множества {2, 4, 8, 6}, которое будет циклически повторяться. Дальше надо понять остаток от деления 1234 на 4. 1234 : 4 = 308 и остаток 2. Значит последния цифра у нас совершит 308 полных циклов и еще 2 шага. Таким образом число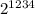
заканчивается на цифру 4. Следовательно 
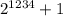заканчивается на цифру 5, а значит это число делится на 5 и как факт является составным.
угловой коэффициент касательной к функции равен значению производной функции в точке касания, т.е. k=y'(x₀)
1) найдем производную:
y'(x)=(x²+4)'=2x
k=y'(x₀)=y'(1)=2*1=2 - угловой коэффициент касательной к графику функции в точке с абсциссой x₀=1
2) теперь известен угловой коэффициент k=4, но неизвестна точка касания x₀, т.е.
y'(x₀)=k
2*x₀=4
x₀=2
чтобы найти ординату точки, подставим x₀ в функцию y(x):
y₀=y(x₀)=2²+4=4+4=8
(2;4) - координаты точки, в которой угловой коэффициент касания равен k=4
3) уравнение касательной в общем виде: f(x)=y(x₀)+y'(x₀)*(x-x₀)
x₀=1, y'(x₀)=2 - найдено выше под 1)
y(x₀)=1²+4=5
подставляем найденные значения в общий вид:
f(x)=5+2(x-1)=5+2x-2=2x+3 - уравнение касательной к графику функции в точке с абсциссой x₀=1