Для логарифма Область Допустимых Значений (она же - ОДЗ) выглядит так (это нам понадобится для решения задачи):
A)
Рассмотрим логарифм . С точки зрения ОДЗ и того, что и , с этим логарифмом все хорошо.
Но, так как основание логарифма меньше единицы, то его значение больше ноля при , а меньше ноля - при . Из данного в задаче условия на имеем, что . Значит, выражение этого логарифма отрицательно.
Но что тогда можно сказать о втором логарифме? Для него подлогарифмическое выражение меньше ноля, что нас абсолютно не устраивает.
Итог: выражение не имеет смысла.
B)
Рассуждаем по аналогии:
- существует и больше ноля (так как и ). Основание и подлогарифмическое выражение не только соответствуют ОДЗ, но и оба меньше единицы.
- тоже существует, так как и , а также подлогарифмическое выражение больше ноля.
Итог: выражение имеет смысл.
C)
Решаем с использованием уже оговоренных схем:
- существует и больше единицы (так как ).
- существует и меньше ноля (так как и ).
- не очень хорошо существует, в силу отрицательности подлогарифмического выражения.
Итог: выражение не имеет смысла.
D)
- существует и меньше ноля (так как и ).
- не существует, так как .
- не существует, так как уже его подлогарифмическое выражение не существует.
А) не имеет. т.к. ㏒ₐ(а+1) отрицательно, и ㏒₂( ㏒ₐ(а+1)) не имеет смысла.
В) ㏒ₐ(π/4) >0; ㏒ₐ(㏒ₐ(π/4)) имеет смысл.
С) ㏒₂3 положительно, ㏒ₐ(㏒₂3) отрицательно. поэтому ㏒₂(㏒ₐ(㏒₂3)) смысла не имеет.
D) (㏒₁₀а) отрицателен, поэтому (㏒₁₀(㏒₁₀а)) уже не имеет смысла, а уж ㏒₁₀(㏒₁₀(㏒₁₀а)) и тем более не имеет смысла.
ответ В)
Дополнение. Если основание логарифма больше 1, а подлогарифмическое значение больше нуля, но меньше 1, то логарифм отрицат. и обратно, а если основание логарифма больше нуля, но меньше 1, и подлогарифмическое значение больше нуля, но меньше 1, то логарифм положителен. или если оба больше единицы.
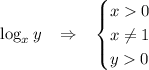
A)Рассмотрим логарифм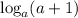 . С точки зрения ОДЗ и того, что
. С точки зрения ОДЗ и того, что 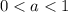 и
и 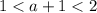 , с этим логарифмом все хорошо.
, с этим логарифмом все хорошо.
Но, так как основание логарифма меньше единицы, то его значение больше ноля при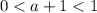 , а меньше ноля - при
, а меньше ноля - при 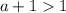 . Из данного в задаче условия на
. Из данного в задаче условия на  имеем, что
имеем, что 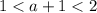 . Значит, выражение этого логарифма отрицательно.
. Значит, выражение этого логарифма отрицательно.
Но что тогда можно сказать о втором логарифме? Для него подлогарифмическое выражение меньше ноля, что нас абсолютно не устраивает.
Итог: выражение не имеет смысла.
B)Рассуждаем по аналогии:
Итог: выражение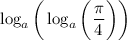 имеет смысл.
имеет смысл.
C)Решаем с использованием уже оговоренных схем:
Итог: выражение не имеет смысла.
D)Итог: выражение не имеет смысла.
ответ : B ) .А) не имеет. т.к. ㏒ₐ(а+1) отрицательно, и ㏒₂( ㏒ₐ(а+1)) не имеет смысла.
В) ㏒ₐ(π/4) >0; ㏒ₐ(㏒ₐ(π/4)) имеет смысл.
С) ㏒₂3 положительно, ㏒ₐ(㏒₂3) отрицательно. поэтому ㏒₂(㏒ₐ(㏒₂3)) смысла не имеет.
D) (㏒₁₀а) отрицателен, поэтому (㏒₁₀(㏒₁₀а)) уже не имеет смысла, а уж ㏒₁₀(㏒₁₀(㏒₁₀а)) и тем более не имеет смысла.
ответ В)
Дополнение. Если основание логарифма больше 1, а подлогарифмическое значение больше нуля, но меньше 1, то логарифм отрицат. и обратно, а если основание логарифма больше нуля, но меньше 1, и подлогарифмическое значение больше нуля, но меньше 1, то логарифм положителен. или если оба больше единицы.