Введем ограничения:
1 случай
тогда логарифм - возрастающая функция
с учетом условия
2 случай
логарифм убывающая функция
с учетом условия : решений нет
Окончательный ответ (с учетом ограничений) (-3;-1)
Введем ограничения:
1 случай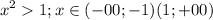
тогда логарифм - возрастающая функция
с учетом условия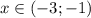
2 случай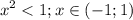
логарифм убывающая функция
с учетом условия : решений нет
Окончательный ответ (с учетом ограничений) (-3;-1)