Ломаная аbc - график некоторой функции, причем a(-4; 2) , b(2 ; -2) и c(4; 4) . начертите график и с его найдите : а) значения функции, соответствующие х =-3,5 ; -2,5 ; 0 ; 1,5 ; 2,5 ; 3. б) значения аргумента которым соответствует у = -1,5; 1; 1,5.
7 м
Объяснение:
Турист находится в точке "Т" (см приложение) и наблюдает основание маяка, расположенного в точке "О", а также вершину маяка, расположенную в точке "В". Точка "Г" - это горизонт, проведенный от туриста до проекции основания маяка.
Треугольники ТГО и ТГВ прямоугольные с прямым углом в точке "Г".
Длина катета прямоугольного треугольника равна длине второго катета умноженного на тангенс противолежащего угла.
ГВ = ТГ * tg(45°) = 15 * 1 = 15 м
ГО = ТГ * tg(30°) = 15 * (√3 / 3) = 5 * 1.7 = 8.5 м
Высота маяка равна:
ГВ - ГО = 15 - 8.5 = 6.5 м
Округлив получаем 7 м
Это решение, если углы указаны в градусах. Почему то в вопросе после 30 стоит знак "секунды"...
(2 + x) (14 − x) = (2x − 8) (1 + 7x)
Чтобы умножить 2+x на 14−x, используйте свойство дистрибутивности и приведение подобных.
28 + 12x − x² = (2x − 8) (1 + 7x)
Чтобы умножить 2x−8 на 1+7x, используйте свойство дистрибутивности и приведение подобных.
28 + 12x − x² = −54x + 14x² − 8
Прибавьте 54x к обеим частям.
28 + 12x − x² + 54x = 14x² − 8
Объедините 12x и 54x, чтобы получить 66x.
28 + 66x − x² = 14x² − 8
Вычтите 14x² из обеих частей уравнения.
28 + 66x − x² − 14x² = −8
Объедините −x² и −14x² , чтобы получить −15x².
28 + 66x − 15x² = −8
Прибавьте 8 к обеим частям.
28 + 66x − 15x² + 8 = 0
Чтобы вычислить 36, сложите 28 и 8.
36 + 66x − 15x² = 0
Все уравнения вида ax² + bx + c = 0 можно решить с формулы корней квадратного уравнения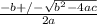
Эта формула дает два решения: одно, когда для ± используется сложение, а второе — когда вычитание.
−15x + 66x + 36 = 0
Данное уравнение имеет стандартный вид ax² +bx+c=0. Подставьте −15 вместо a, 66 вместо b и 36 вместо c в формуле корней квадратного уравнения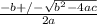
x₁ =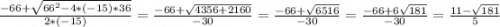
x₂ =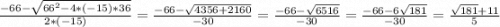
ответ: