60 м и 50 м.
Объяснение:
Длина забора - это периметр прямоугольника. Сумма длины и ширины - половина периметра, 220 : 2 = 110 (м).
Пусть ширина прямоугольника равна х м, тогда длина прямоугольника равна (110 - х) м.
Зная, что площадь равна 3000 м², составим и решим уравнение:
х(110 - х) = 3000
- х² + 110х - 3000 = 0
х² - 110х + 3000 = 0
D = 12100 - 12000 = 100
x1 = (110+10)/2 = 60;
x2 = (110-10)/2 = 50.
Если длина больше ш рины, то она равна 60 м, тогда
110 - 60 = 50 (м) - ширина прямоугольника.
ответ: 60 м и 50 м.
Если каждое слагаемое делится на некоторое число, то и вся сумма делится на это число.
Если одно слагаемое делится на некоторое число, а другое слагаемое не делится на это число, то и вся сумма не делится на это число.
1.
Пусть - пять последовательных натуральных чисел, тогда их сумма равна:
Очевидно, что каждое слагаемое и делится на 5, а это означает, что вся сумма делится на 5.
Доказано.
2.
Пусть - четыре последовательных натуральных числа, тогда их сумма равна:
Очевидно, что первое слагаемое делится на 4, а второе слагаемое не делится на 4, это означает, что вся сумма не делится на 4.
3.
Пусть - четыре последовательных нечётных натуральных числа, тогда их сумма равна:
Очевидно, что каждое слагаемое и делится на 8, а это означает, что вся сумма делится на 8.
4.
Пусть ; - четыре последовательных чётных натуральных числа, тогда их сумма равна:
Очевидно, что каждое слагаемое и делится на 4, а это означает, что вся сумма делится на 4.
60 м и 50 м.
Объяснение:
Длина забора - это периметр прямоугольника. Сумма длины и ширины - половина периметра, 220 : 2 = 110 (м).
Пусть ширина прямоугольника равна х м, тогда длина прямоугольника равна (110 - х) м.
Зная, что площадь равна 3000 м², составим и решим уравнение:
х(110 - х) = 3000
- х² + 110х - 3000 = 0
х² - 110х + 3000 = 0
D = 12100 - 12000 = 100
x1 = (110+10)/2 = 60;
x2 = (110-10)/2 = 50.
Если длина больше ш рины, то она равна 60 м, тогда
110 - 60 = 50 (м) - ширина прямоугольника.
ответ: 60 м и 50 м.
Если каждое слагаемое делится на некоторое число, то и вся сумма делится на это число.
Если одно слагаемое делится на некоторое число, а другое слагаемое не делится на это число, то и вся сумма не делится на это число.
1.
Пусть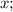
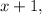
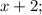
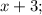
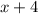- пять последовательных натуральных чисел, тогда их сумма равна:
Очевидно, что каждое слагаемое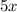
и 
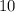делится на 5, а это означает, что вся сумма делится на 5.
Доказано.
2.
Пусть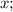
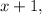
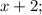
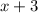- четыре последовательных натуральных числа, тогда их сумма равна:
Очевидно, что первое слагаемое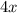
делится на 4, а второе слагаемое 
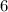не делится на 4, это означает, что вся сумма не делится на 4.
Доказано.
3.
Пусть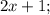
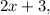
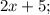
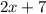- четыре последовательных нечётных натуральных числа, тогда их сумма равна:
Очевидно, что каждое слагаемое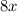
и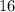 
делится на 8, а это означает, что вся сумма делится на 8.
Доказано.
4.
Пусть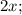
; 
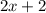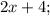
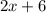- четыре последовательных чётных натуральных числа, тогда их сумма равна:
Очевидно, что каждое слагаемое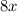
и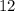 
делится на 4, а это означает, что вся сумма делится на 4.
Доказано.