Если не учитывать, что 100% тоже больше 94%, то: Пусть х - число домов в этом районе, а х-1 - число домов, имеющих больше 5 этажей (чтобы найти минимально значение х, разница между числом домов, имеющих больше 5 этажей, и общим числом домов должна быть минимальна)
Получаем уравнение:
Проверка подбором
11 домов имеют больше 5 этажей 12 домов всего 11 / 12 = 0,91(6) = 91,(6)% Не подходит.
... 15 домов имеют больше 5 этажей 16 домов всего 15 / 16 = 0,9375 = 93,75% Не подходит.
16 домов имеют больше 5 этажей 17 домов всего 16 / 17 = 0,941176... = 94,1176...% Подходит.
ответ: 17 - наименьшее число домов в данном районе.
Последнюю вероятность (того, что попали ровно 2 раза) можно посчитать точно также, а можно просто воспользоваться тем, что сумма вероятностей должна быть равной единице
Если не учитывать, что 100% тоже больше 94%, то:
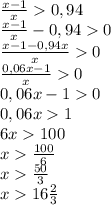
Пусть х - число домов в этом районе, а х-1 - число домов, имеющих больше 5 этажей
(чтобы найти минимально значение х, разница между числом домов, имеющих больше 5 этажей, и общим числом домов должна быть минимальна)
Получаем уравнение:
Проверка подбором
11 домов имеют больше 5 этажей
12 домов всего
11 / 12 = 0,91(6) = 91,(6)%
Не подходит.
...
15 домов имеют больше 5 этажей
16 домов всего
15 / 16 = 0,9375 = 93,75%
Не подходит.
16 домов имеют больше 5 этажей
17 домов всего
16 / 17 = 0,941176... = 94,1176...%
Подходит.
ответ: 17 - наименьшее число домов в данном районе.
Сначала то, что попроще:
0 раз: вероятность (1-0,8)*(1-0,7)*(1-0,6)=0,024
3 раза: вероятность 0,8*0,7*0,6=0,336
Теперь, например, посчитаем вероятность того, что попали ровно 1 раз, т.е. попал один из них, а все остальные промахнулись:
0,8*(1-0,7)(1-0,6) + 0,7*(1-0,8)(1-0,6) + 0,6*(1-0,8)(1-0,7)=0,188
Последнюю вероятность (того, что попали ровно 2 раза) можно посчитать точно также, а можно просто воспользоваться тем, что сумма вероятностей должна быть равной единице
1-0,336-0,024-0,188=0,452
0,8*0,7*(1-0,6)+0,8*(1-0,7)*0,6+(1-0,8)*0,7*0,6=0,452