Мы видим так называемую симметрическую систему уравнений(при замене переменных друг на друг, система не изменится. Для такой системы есть стандартная замена xy=t, x+y=k
, тогда перепишем как. Теперь нужно представить уравнение в первой строке системы через новые переменные, для этого попробуем выделить полный квадрат, x²+y² из этой суммы можно получить 2 вида квадрата, квадрат суммы и квадрат разности, нам выгодно сделать сумму, тогда добавим 2xy, но чтобы ничего не изменилось вычтем 2xy. Тогда (x²+2xy+y²)-2xy=5. Свернем (x+y)²-2xy=5. Теперь мы видим наши замены в чистом виде 1-ая строка = k²-2t=5.
. Теперь перейдем к следующему. из второго уравнения вычтем t из обеих частей, тогда k=5-t. и подставим это значение k в первое.
Расскроем скобки, t²-10t+25-2t-5=0
t²-12t+20=0. Получили квадратное уравнение, которое решаем любым удобным (для меня Т. обратная Т.Виета)
t=10 или t=2. удобнее записать так =10 =2, отсюда найдем
=5-=5-10=-5, =5-=5-2=3.
Теперь обратные замены в 2 системы
. опять замена), x=-5-y., -5y-y²=10,y²+5y+10=0, D=25-40,эта система решений не имеет( на множестве действительных чисел)
. Опять замена x=3-y. 3y-y²=2, y²-3y+2,тогда =2,=1. Тогда =1,=2. Что не удивительно, т.к. в симметрических системах достаточно получить ответ лишь для одной переменной и просто поменять местами с другой, но мы в этом, так сказать, убедились.
Для того, чтобы решать такие уравнения, нужно раскрыть скобки(если они есть), а затем перенести в правую часть числовые значения, а в левой оставить с переменными (x, y и т.д.). При переносе из одной стороны в другую знаки меняются. После нужно делить обе части на число при переменной(в данном случае на число перед х). Если можно как-то сократить полученное, сокращаем. Если можно выделить целую часть - выделяем. Б) -16х = 4 х = (можно сократить) х = В) 5х - 9 = 14 + 3х 5х - 3х = 14 + 9 2х = 23 х = 11,5 Г) 5х - 7 = 10 5х = 10 + 7 5х = 17 х = х = Д) 2(х - 3) = -7(1 - х) 2х - 6 = -7 + 7х 2х - 7х = -7 + 6 -5х = 1 х = Е) 1 - 3(х - 1) = 2 - 7(1 - х) 1 - 3х +3 = 2 - 7 + 7х -3х - 7х = -5 - 3 - 1 -10х = -9 х = (т.к. в числителе и в знаменателе было по минусу, то всего минуса было два, а два минуса дали плюс).
(1;2) (2;1)
Объяснение:
Мы видим так называемую симметрическую систему уравнений(при замене переменных друг на друг, система не изменится. Для такой системы есть стандартная замена xy=t, x+y=k
, тогда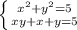
перепишем как
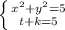. Теперь нужно представить уравнение в первой строке системы через новые переменные, для этого попробуем выделить полный квадрат, x²+y² из этой суммы можно получить 2 вида квадрата, квадрат суммы и квадрат разности, нам выгодно сделать сумму, тогда добавим 2xy, но чтобы ничего не изменилось вычтем 2xy. Тогда (x²+2xy+y²)-2xy=5. Свернем (x+y)²-2xy=5. Теперь мы видим наши замены в чистом виде 1-ая строка = k²-2t=5.
t²-12t+20=0. Получили квадратное уравнение, которое решаем любым удобным (для меня Т. обратная Т.Виета)
t=10 или t=2. удобнее записать так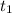
=10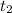 
=2, отсюда найдем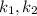 
Теперь обратные замены в 2 системы
ответ 2 пары чисел (1;2) (2;1)
Б) -16х = 4
х =
х =
В) 5х - 9 = 14 + 3х
5х - 3х = 14 + 9
2х = 23
х = 11,5
Г) 5х - 7 = 10
5х = 10 + 7
5х = 17
х =
х =
Д) 2(х - 3) = -7(1 - х)
2х - 6 = -7 + 7х
2х - 7х = -7 + 6
-5х = 1
х =
Е) 1 - 3(х - 1) = 2 - 7(1 - х)
1 - 3х +3 = 2 - 7 + 7х
-3х - 7х = -5 - 3 - 1
-10х = -9
х =