Мастер должен был выполнить заказ на изготовление 160 деталей. Он изготавливал в день на 2 детали больше, чем планировал, и выполнил заказ на 4 дня раньше поставленного срока. Сколько деталей в день изо- тавливал мастер?
Из условия о том, что каких бы двух мальчиков мы ни взяли, у них будет разное количество подруг, можно сделать вывод, что число подруг у каждого мальчика уникальное.
Итак, число подруг у мальчиков уникальное и равно некоторому числу от 1 до N (всего N вариантов). Но в классе есть только N мальчиков. Значит, в классе есть ровно один мальчик с одной подругой, ровно один мальчик с двумя подругами, ровно один мальчик с тремя подругами, и т.д, ровно один мальчик с N подругами.
Тогда пары будем формировать следующим образом:
1. Берем мальчика с одной подругой и ставим его в пару с этой подругой.
2. Далее берем мальчика с двумя подругами. На данный момент только одна девочка занята в парах, поэтому пару для этого мальчика из двух подруг мы найти точно сможем.
3. На следующих шагах мы последовательно выбираем мальчика с K подругами (где K = 3, 4, ...) и обнаруживаем, что к этому моменту в пары распределена только (K-1) девочка. Значит, найдется такая девочка, которую можно будет поставить этому мальчику в пару.
4. На последнем шаге мы возьмем мальчика, у которого есть N подруг (то есть все девочки класса). Но только (N-1) девочка уже занята в парах. Значит одна оставшаяся девочка будет парой для последнего мальчика.
Пусть в классе N мальчиков и N девочек.
Из условия о том, что каких бы двух мальчиков мы ни взяли, у них будет разное количество подруг, можно сделать вывод, что число подруг у каждого мальчика уникальное.
Итак, число подруг у мальчиков уникальное и равно некоторому числу от 1 до N (всего N вариантов). Но в классе есть только N мальчиков. Значит, в классе есть ровно один мальчик с одной подругой, ровно один мальчик с двумя подругами, ровно один мальчик с тремя подругами, и т.д, ровно один мальчик с N подругами.
Тогда пары будем формировать следующим образом:
1. Берем мальчика с одной подругой и ставим его в пару с этой подругой.
2. Далее берем мальчика с двумя подругами. На данный момент только одна девочка занята в парах, поэтому пару для этого мальчика из двух подруг мы найти точно сможем.
3. На следующих шагах мы последовательно выбираем мальчика с K подругами (где K = 3, 4, ...) и обнаруживаем, что к этому моменту в пары распределена только (K-1) девочка. Значит, найдется такая девочка, которую можно будет поставить этому мальчику в пару.
4. На последнем шаге мы возьмем мальчика, у которого есть N подруг (то есть все девочки класса). Но только (N-1) девочка уже занята в парах. Значит одна оставшаяся девочка будет парой для последнего мальчика.
Відповідь:
Пояснення:
1.
Cоставляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:
r^2 +2 r + 5 = 0
D=2^2 - 4·1·5=-16
Корни характеристического уравнения: (комплексные корни):
r1 = -1 + 2i
r2 = -1 - 2i
Общее решение однородного уравнения имеет вид:
y- = C1 e^(-x) cos(2x) + C2 e^(-x) cos(2x) , Ci ∈ R
Рассмотрим правую часть:
f(x) = -2*sin(x)
Здесь P(x) = 0, Q(x) = -2, α = 0, β = 1.
Следовательно, число α + βi = i не является корнем характеристического уравнения.
Уравнение имеет частное решение вида:
y· = Acos(x) + Bsin(x)
Вычисляем производные:
y' = -A·sin(x)+B·cos(x)
y'' = -(A·cos(x)+B·sin(x))
которые подставляем в исходное дифференциальное уравнение:
y'' + 2y' + 5y = (-(A·cos(x)+B·sin(x))) + 2(-A·sin(x)+B·cos(x)) + 5(Acos(x) + Bsin(x)) = -2·sin(x)
или
-2·A·sin(x)+4·A·cos(x)+4·B·sin(x)+2·B·cos(x) = -2·sin(x)
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
1: -2A + 4B = -2
1: 4A + 2B = 0
Решая ее, находим:
A = 1/5;B = -2/5;
Частное решение имеет вид:
y·=1/5cos(x) -2/5sin(x)
Таким образом, общее решение дифференциального уравнения имеет вид:
y = y- +y. = y- = C1 e^(-x) cos(2x) + C2 e^(-x) cos(2x) +1/5cos(x) -2/5sin(x)
2.
Cоставляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:
r^2 +0 r - 3 = 0
D=0^2 - 4·1·(-3)=12
Корни характеристического уравнения:
r1 =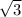
r2 =-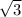
Общее решение однородного уравнения имеет вид:
y- = C1e^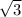 +C2 e^ (-
+C2 e^ (-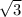 ) , Ci ∈ R
) , Ci ∈ R
Рассмотрим правую часть:
f(x) = (4*x+1)*e^(2*x)
Поиск частного решения.
Здесь P(x) = 4•x+1, Q(x) = 0, α = 2, β = 0.
Следовательно, число α + βi = 2 + 0i не является корнем характеристического уравнения.
Уравнение имеет частное решение вида:
y· = (Ax + B)e^(2x)
Вычисляем производные:
y' = A·e^(2x+2(A·x+B)·e^(2x)
y'' = 4(A·x+A+B)·e^(2x)
которые подставляем в исходное дифференциальное уравнение:
y'' -3y = (4(A·x+A+B)·e^(2x)) -3((Ax + B)e^(2x)) = (4·x+1)·e^(2·x)
или
A·x·e^(2x)+4·A·e^(2x)+B·e^(2x) = (4·x+1)·e^(2·x)
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
x: A = 4
1: 4A + B = 1
Решая ее, находим:
A = 4;B = -15;
Частное решение имеет вид:
y·=(4x -15)e^(2x)
Таким образом, общее решение дифференциального уравнения имеет вид:
y = y- +y. = C1e^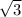 +C2 e^ (-
+C2 e^ (-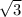 ) +(4x -15)e^(2x).
) +(4x -15)e^(2x).