Материальная точка движется по закону х(t)=3t^-t^2+5t найти скорость и ускорение в момент t=2 в начале движения.

Показать ответ

Ответ:

masha32434

14.02.2021 14:45

A₁ = 5, аn + 1= an + 3
a₂ = 5 + 3 = 8
d = 3
a₁₂ = 5 + 3(12-1) = 5 + 33 = 38
a₃₄ = 5 + 3(34-1) = 5 + 99 = 104

a₁ = 84, d = -5
a₃₇ = 84 - 5(37-1) = -96
a₆₀ = 84 - 5(60-1) = -211

-67; -60; -53...
а₁ = -67
d = 7
S₅₂ = 2a₁ + d(n-1)*n / 2 = 2*(-67) + 7(52-1)*52 / 2 = -134 + 18564 / 2 = 9215

an = 5n - 4
a₁ = 5*1 - 4 = 1
a₂ = 5*2 - 4 = 6
d = 5
S₁₅₀ = 2a₁ + d(n-1)*n / 2 = 2*1 + 5(150-1)*150 / 2 = 2 + 111750 / 2 = 55876

a₁ = 32, а₆₁ = -58
a₆₁ = 32 + d(61-1) = 32 + 60d
-58 = 32 + 60d
60d = -90
d = -1,5
-36 = 32 - 1,5(n-1)
-36 = 32 -1,5n + 1,5
-36 = 33,5 - 1,5n
-69,5 = 1,5n
n = -69,5/1,5 - не является

8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96, 104, 112, 120, 128, 136, 144, 152, 160, 168, 176, 184, 192, 200, 208, 216, 224, 232, 240, 248, 256, 264, 272, 280, 288, 296, 304, 312, 320, 328, 336, 344.
S = 7568

0,0(0 оценок)

Ответ:

yardeebro

01.10.2022 15:25

1. Решим первое неравенство этой системы:

5 - 5x 11

-5x 11 - 5

-5x 6

$x < -\dfrac{6}{5}$

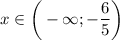
ответ: $x \in \bigg(-\infty; -\dfrac{6}{5} \bigg)$

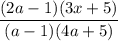2. Дробь $\dfrac{(2a-1)(3x+5)}{(a-1)(4a+5)}$ существует, если

$(a-1)(4a+5) \neq 0\\ \\\left[\begin{array}{ccc}a-1\neq0 \ \\4a+5\neq0 \\ \end{array}\right \ \ \ \ \ \ \ \left[\begin{array}{ccc}a\neq1 \ \ \ \\ a\neq -\dfrac{5}{4} \\ \end{array}\right$

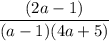Перед тем как выражать , нужно рассмотреть случаи, когда дробь $\dfrac{(2a-1)}{(a-1)(4a+5)}$ положительная, а когда отрицательная:

Если такая дробь положительная, то при нахождении переменной

знак неравенства меняться не будет (так как делим (умножаем) на положительное число):

$\dfrac{2a-1}{(a-1)(4a+5)} 0$

Решим неравенство методом интервалов.

а) ОДЗ: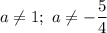 $a\neq 1; \ a\neq -\dfrac{5}{4}$

б) Нуль неравенства: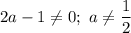 $2a-1 \neq 0; \ a \neq \dfrac{1}{2}$

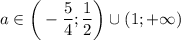в) Решением данного неравенства будет $a \in \bigg(-\dfrac{5}{4}; \dfrac{1}{2} \bigg) \cup (1; +\infty )$ .

При таких значениях параметра знак неравенства меняться не будет:

$\dfrac{(2a-1)(3x+5)}{(a-1)(4a+5)} 1 \ \ \ \ \bigg| : \dfrac{2a-1}{(a-1)(4a+5)}$

$3x+5 \dfrac{(a-1)(4a+5)}{2a-1}$

$3x \dfrac{(a-1)(4a+5)}{2a-1} - 5$

$3x \dfrac{4a^{2} + 5a - 4a - 5 - 5(2a-1)}{2a-1}$

$3x \dfrac{4a^{2} + a - 5 - 10a + 4}{2a - 1}$

$3x \dfrac{4a^{2} - 9a}{2a-1} \ \ \ \ \ \ | : 3$

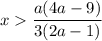
$x \dfrac{a(4a-9)}{3(2a - 1)}$

Если такая дробь отрицательная, то при нахождении переменной

знак неравенства измениться на противоположный (так как делим (умножаем) на отрицательное число):

$\dfrac{2a-1}{(a-1)(4a+5)} < 0$

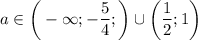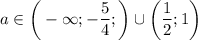Решим неравенство методом интервалов. Решением данного неравенства будет $a \in \bigg(-\infty; -\dfrac{5}{4}; \bigg) \cup \bigg(\dfrac{1}{2} ; 1 \bigg)$ .

При таких значениях параметра знак неравенства изменится:

$\dfrac{(2a-1)(3x+5)}{(a-1)(4a+5)} 1 \ \ \ \ \bigg| : \dfrac{2a-1}{(a-1)(4a+5)}$

$3x+5 < \dfrac{(a-1)(4a+5)}{2a-1}$

$x < \dfrac{a(4a-9)}{3(2a - 1)}$

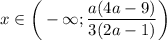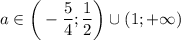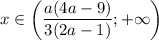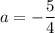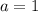ответ: если $a \in \bigg(-\infty; -\dfrac{5}{4}; \bigg) \cup \bigg(\dfrac{1}{2} ; 1 \bigg)$ , то $x \in \bigg (-\infty; \dfrac{a(4a-9)}{3(2a - 1)} \bigg)$ ; если $a \in \bigg(-\dfrac{5}{4}; \dfrac{1}{2} \bigg) \cup (1; +\infty )$ , то $x \in \bigg (\dfrac{a(4a-9)}{3(2a - 1)}; + \infty \bigg)$ ; если $a = -\dfrac{5}{4}$ и a = 1 , то неравенство не имеет решений.

3. Данная система неравенств решается в зависимости от значений параметра , поэтому:

1) Рассмотрим случай, когда решение неравенств пересекается:

Если $\dfrac{a(4a-9)}{3(2a - 1)} < -\dfrac{6}{5}$ , то есть $a \in \bigg(-\infty; -\dfrac{3}{4} \bigg) \cup \bigg(\dfrac{1}{2}; \dfrac{6}{5}\bigg)$ , то в объединении с $a \in \bigg(-\dfrac{5}{4}; \dfrac{1}{2} \bigg) \cup (1; +\infty )$ получаем $a \in \bigg(-\dfrac{5}{4}; - \dfrac{3}{4}\bigg) \cup \bigg(1; \dfrac{6}{5} \bigg)$ $x < \dfrac{a(4a-9)}{3(2a - 1)}$ при $a \in \bigg(-\infty; -\dfrac{5}{4}; \bigg) \cup \bigg(\dfrac{1}{2} ; 1 \bigg)$ Если $\dfrac{a(4a-9)}{3(2a - 1)} -\dfrac{6}{5}$ , то есть $a \in \bigg(-\dfrac{3}{4}; \dfrac{1}{2} \bigg)\cup \bigg(\dfrac{6}{5}; + \infty \bigg)$ , то в объединении с $a \in \bigg(-\infty; -\dfrac{5}{4}; \bigg) \cup \bigg(\dfrac{1}{2} ; 1 \bigg)$ получаем, что таких

не существует, то есть такого варианта эта система не имеет.

2) Рассмотрим случай, когда решение неравенств не пересекается (когда система не имеет решений):

Оставшийся промежуток является решением этого варианта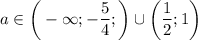: $a \in \bigg[-\dfrac{3}{4}; \dfrac{1}{2} \bigg]\cup \bigg[\dfrac{6}{5}; + \infty \bigg) \cup \begin{Bmatrix} -\dfrac{5}{4}; 1 \end{Bmatrix}$

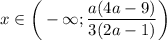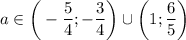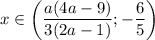ответ: если $a \in \bigg(-\infty; -\dfrac{5}{4}; \bigg) \cup \bigg(\dfrac{1}{2} ; 1 \bigg)$ , то $x \in \bigg (-\infty; \dfrac{a(4a-9)}{3(2a - 1)} \bigg)$ ; если $a \in \bigg(-\dfrac{5}{4}; - \dfrac{3}{4}\bigg) \cup \bigg(1; \dfrac{6}{5} \bigg)$ , то $x \in \bigg (\dfrac{a(4a-9)}{3(2a - 1)}; -\dfrac{6}{5} \bigg)$ ; если $a \in \bigg[-\dfrac{3}{4}; \dfrac{1}{2} \bigg]\cup \bigg[\dfrac{6}{5}; + \infty \bigg) \cup \begin{Bmatrix} -\dfrac{5}{4}; 1 \end{Bmatrix}$ , то система не имеет решений.