Среди всех троек , являющихся решением исходного уравнения выберем тройку такую, что сумма минимальна. Если существует более одной такой тройки, то выберем любую.
Рассмотрим уравнение по модулю 3: , что возможно только если делятся на 3. Пусть тогда . Имеем: , откуда ясно, что , откуда , поэтому . Подставим в уравнение: . То есть любому решению можно сопоставить решение , причем . Но для рассматриваемого решения сумма квадратов минимальна. Следовательно , что возможно только в случае, если , откуда следует .
Среди всех троек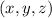 , являющихся решением исходного уравнения выберем тройку
, являющихся решением исходного уравнения выберем тройку 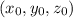 такую, что сумма
такую, что сумма 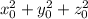 минимальна. Если существует более одной такой тройки, то выберем любую.
минимальна. Если существует более одной такой тройки, то выберем любую.
Рассмотрим уравнение по модулю 3: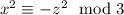 , что возможно только если
, что возможно только если 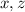 делятся на 3. Пусть тогда
делятся на 3. Пусть тогда 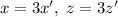 . Имеем:
. Имеем: 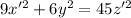 , откуда ясно, что
, откуда ясно, что 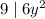 , откуда
, откуда 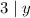 , поэтому
, поэтому 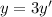 . Подставим в уравнение:
. Подставим в уравнение: 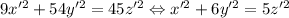 . То есть любому решению
. То есть любому решению 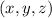 можно сопоставить решение
можно сопоставить решение 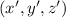 , причем
, причем 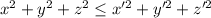 . Но для рассматриваемого решения сумма квадратов минимальна. Следовательно
. Но для рассматриваемого решения сумма квадратов минимальна. Следовательно 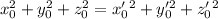 , что возможно только в случае, если
, что возможно только в случае, если 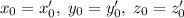 , откуда следует
, откуда следует 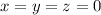 .
.