Тут следует сказать, что минимум функции все-таки определяется наличием нуля в производной. То есть минимум - будет критической точкой. А вот наименьшее значение функции - обычно это понятие применяется, если речь ведут об отрезке или интервале (как конечном так и бесконечном). Насчет минимума функции - не знаю случаев, когда он не достижим. Насчет наименьшего значения - этого утверждать не могу. Он может и не достигаться.
Например.
Найдем производную.
Производную приравняем нулю
В точке х=3 производная меняет знак с минуса на плюс (это минимум),
Значение функции равно (-8).
В точке производная меняет знак с плюса на минус - это максимум.
А вот наименьшее значение функции на всей оси недостижимо. Это при .
Тут следует сказать, что минимум функции все-таки определяется наличием нуля в производной. То есть минимум - будет критической точкой. А вот наименьшее значение функции - обычно это понятие применяется, если речь ведут об отрезке или интервале (как конечном так и бесконечном). Насчет минимума функции - не знаю случаев, когда он не достижим. Насчет наименьшего значения - этого утверждать не могу. Он может и не достигаться.
Например.
Найдем производную.
Производную приравняем нулю
В точке х=3 производная меняет знак с минуса на плюс (это минимум),
Значение функции равно (-8).
В точке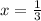 производная меняет знак с плюса на минус - это максимум.
производная меняет знак с плюса на минус - это максимум.
А вот наименьшее значение функции на всей оси недостижимо. Это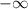 при
при 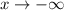 .
.