Алгебра: Ml+mb+sl+sb көпмүшесін көбейткіштерге жікте.

Ml+mb+sl+sb көпмүшесін көбейткіштерге жікте.

Показать ответ

Ответ:

megachiglakov

23.03.2023 06:06

22. -2

23. 1

Объяснение:

22. Рассмотрим каждое из подкоренных выражений:

$2x^2+8x+72=2x^2+8x+8+64=2(x^2+4x+4)+64=2(x+2)^2+64\\3x^2+12x+12=3(x^2+4x+4)=3(x+2)^2\\12-4x-x^2=16-4-4x-x^2=16-(x^2+4x+4)=16-(x+2)^2$

Поскольку квадрат какого-либо числа неотрицателен,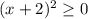 $(x+2)^2\geq 0$ , отсюда:

$2(x+2)^2+64\geq 2\cdot 0+64=64\\3(x+2)^2\geq 3\cdot 0=0\\16-(x+2)^2\leq 16-0=16$

Значит, левая часть $\sqrt[3]{2x^2+8x+72}+\sqrt[3]{3x^2+12x+12}\geq \sqrt[3]{64}+\sqrt[3]{0}=4$

Правая часть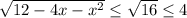 $\sqrt{12-4x-x^2}\leq \sqrt{16}\leq 4$

Левая часть не меньше 4, а правая не больше 4. Значит, равенство достигается тогда и только тогда, когда обе части равны 4. Правая часть равна 4:

$\sqrt{16-(x+2)^2}=4\\16-(x+2)^2=16\\(x+2)^2=0\\x=-2$

Проверим этот корень для левой части:

$\sqrt[3]{2(-2+2)^2+64}+\sqrt[3]{3(-2+2)^2}=\sqrt[3]{64}+\sqrt[3]{0}=4$ — верно.

Уравнение имеет единственный корень x = -2.

23. Заметим, что $(\sqrt{x+8}+\sqrt{x})(\sqrt{x+8}-x)=\sqrt{x+8}^2-\sqrt{x}^2=x+8-x=8$

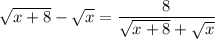Значит, $\sqrt{x+8}-\sqrt{x}=\dfrac{8}{\sqrt{x+8}+\sqrt{x}}$ (знаменатель не обращается в ноль, так как x ≥ 0 по ОДЗ, значит, $\sqrt{x+8}+\sqrt{x}\geq \sqrt{0+8}+\sqrt{0}=\sqrt{8}0$ ).

Пусть $\sqrt{x+8}+\sqrt{x}=t$ . Тогда уравнение имеет вид:

$t^3-\left(\dfrac{8}{t}\right)^2=60\\t^3-\dfrac{64}{t^2}-60=0\\\dfrac{t^5-60t^2-64}{t^2}=0|\cdot t^2\neq 0\\t^5-60t^2-64=0$

Заметим, что t = 4 — корень многочлена левой части. Поделив его столбиком на (t - 4), получим его разложение на множители:

(t-4)(t^4+4t^3+16t^2+4t+16)=0

Поскольку t > 0, $t^4+4t^3+16t^2+4t+160^4+4\cdot 0^3+16\cdot 0^2+4\cdot 0 +16=160$ , значит, обе части можно поделить на второй множитель, так как он не равен нулю. Получаем:

$t-4=0\\t=4\\\sqrt{x+8}+\sqrt{x}=4\\(\sqrt{x+8}+\sqrt{x})^2=4^2\\x+8+2\sqrt{x+8}\sqrt{x}+x=16\\2\sqrt{x^2+8x}=8-2x$

Левая часть неотрицательна, значит, правая часть также неотрицательна: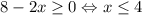 $8-2x\geq 0\Leftrightarrow x\leq 4$

$(2\sqrt{x^2+8x})^2=(8-2x)^2\\4x^2+32x=64-32x+4x^2\\64x=64\\x=1$

Корень удовлетворяет условиям 0 ≤ x ≤ 4, значит, он подходит.

0,0(0 оценок)

Ответ:

gubkaBob216

30.11.2021 08:00

Не люблю проценты. Избавляемся от них. Собираемся взять 100x 1-го сплава, 100y второго, 100z третьего. Ясно, что y>0 - иначе не получить 20% меди.
1 сплав: 60x; 15x; 25x это я указываю количество каждого вещества.
2 сплав: 0y; 30y; 70y
3 сплав: 45z; 0z; 55z

Общий сплав: 100(x+y+z), меди в нем 15x+30y; по условию медь составляет 20%, то есть одну пятую часть сплава:

15x+30y=20(x+y+z); 3x+6y=4x+4y+4z; x=2y-4z.

Поскольку y>0, можно считать, что y=1; x=2-4z.

Естественные ограничения дают такие условия:

x∈[0;2]; z∈[0;1/2]

Нас спрашивают про содержание алюминия, то есть про возможные значения

(60x+45z)/(100x+100y+100z)=(12x+9z)/20x+20y+20z)=║подставляем y=1; x=2-4z║=(24-48z+9z)/40-80z+20+20z)=
(24 -39z)/(60-60z)=(8-13z)/(20(1-z))=
(13(1-z)-5)/(20(1-z))=13/20+1/(4(z-1)); z∈[0;1/2]

Получившаяся функция на этом промежутке убывает⇒ наибольшее значение принимает в левом конце, наименьшее в правом.

Подставив z=0, получаем 13/20-1/4=8/20=2/5, то есть 40%
Подставив z=1/2, получаем 13/20 - 1/2=3/20, то есть 15%

ответ: процентное содержание алюминия от 15% до 40%

0,0(0 оценок)

Популярные вопросы: Алгебра